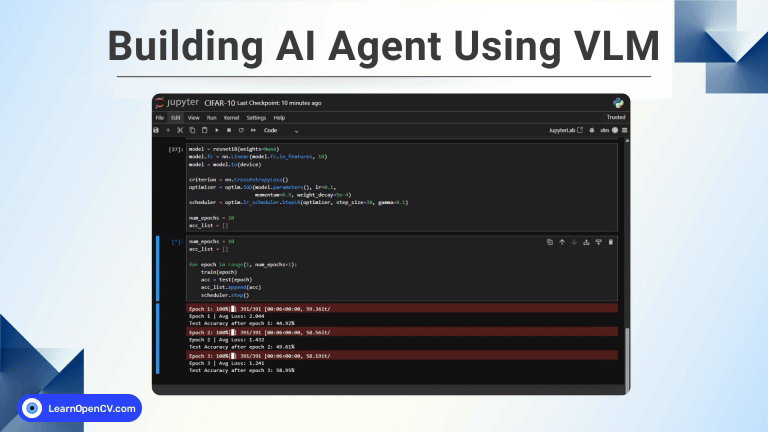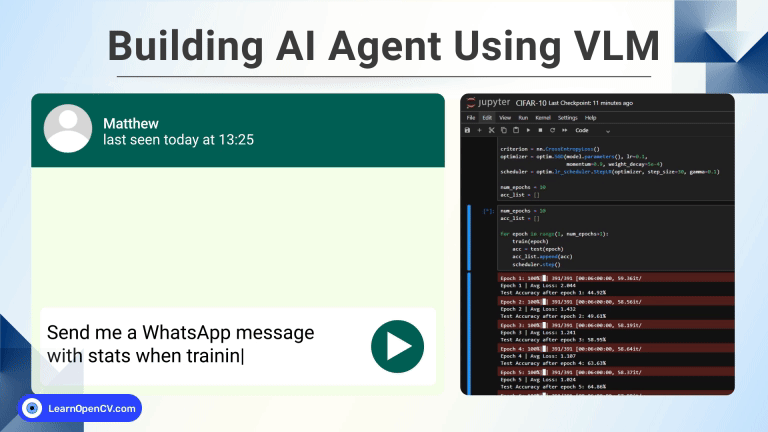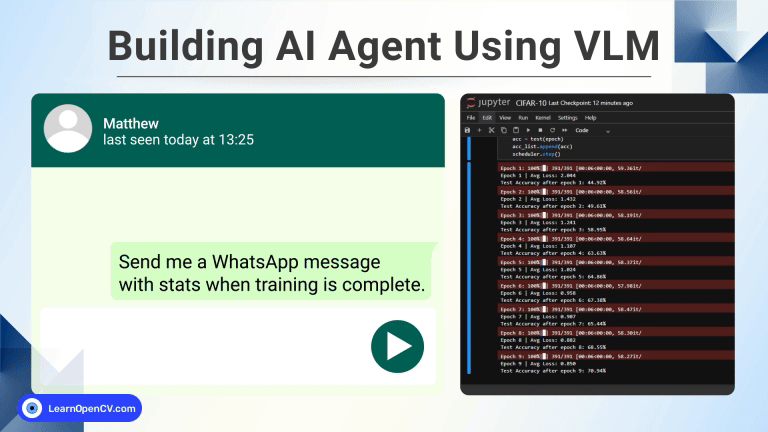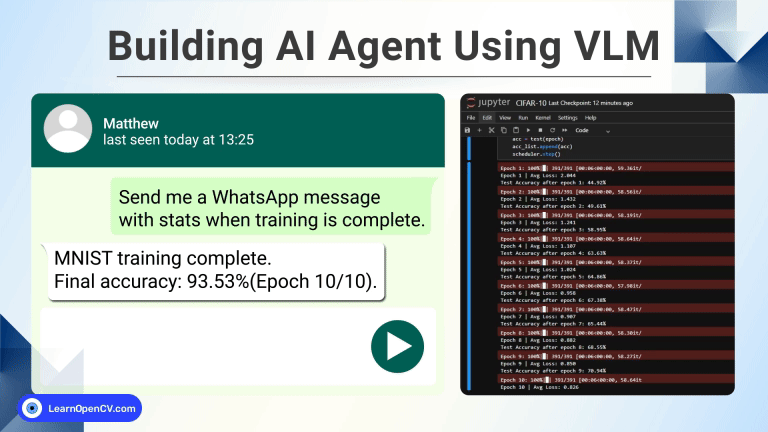
Weighted box fusion: The post-processing step is a trivial yet important component in object detection. In this article, we will demonstrate the significance of Weighted Boxes Fusion (WBF) as opposed to traditional Non-Maximum Suppression (NMS) as a post-processing step in object detection when we have an ensemble of multiple object detection models at our disposal.
Object Detection Models conventionally use Non-Maximum Suppression (NMS) as the default post-processing step to filter out redundant bounding boxes. However, this approach fails to efficiently give unified, averaged predictions across multiple models since they tend to remove less confident boxes having a significant overlap.
To mitigate this problem, we shall discuss an efficient pre-processing step called Weighted Boxes Fusion (WBF) that helps achieve a unified localized prediction across multiple detections.
- Non-Maximum Suppression in Object Detection
- Pitfalls in Non-Maximum Suppression
- Weighted Boxes Fusion: an Effective Post-Processing Approach
- Code Explanation for Weighted Boxes Fusion and Non-Maximum Suppression
- Conclusion
- References
Non-Maximum Suppression in Object Detection
Let’s first get an idea of what Non-Maximum Suppression (NMS) is and why we need it before we take an in-depth look into Weighted Boxes Fusion.
Object detection models usually give multiple predictions over each object instance within an image with some extent of overlaps. This becomes undesirable, so removing these spurious bounding boxes and retaining the most confident box for each instance is imperative. Non-Maximum Suppression helps us achieve this task.
The following figure illustrates the NMS, with multiple predictions across various objects.
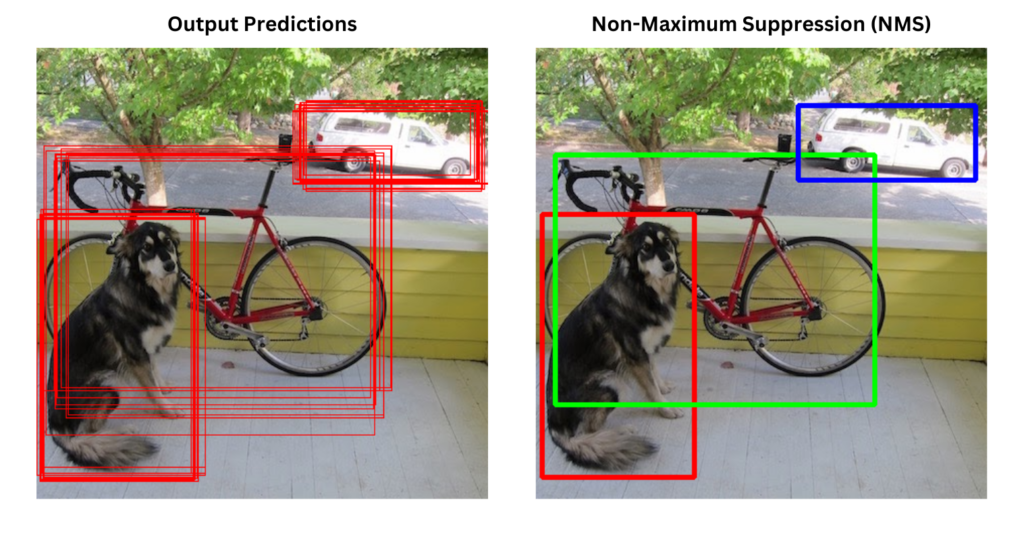
The criteria to filter out these predictions is based on the Intersection over Union (IoU) overlap, also known as the Jaccard overlap. The Intersection over Union (IoU) in Object Detection & Segmentation article discusses an in-depth explanation and implementation of IOU.
The confidence score update for NMS is computed using the following inequations:
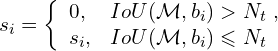
Here, M denotes the prediction with the highest confidence, Nt denotes the IoU threshold (also called the NMS threshold), and si and bi denote the ith, confidence score, and predicted bounding box, respectively.
Therefore, NMS considers only the most confident box for detections belonging to the same object while ignoring the rest.
Pitfalls in Non-Maximum Suppression
Intuitively, lower confidence predictions may capture some latent information that is otherwise ignored by the more confident predictions.
Consider the predictions represented by the dotted lines in the image below.
The predictions capturing the upper torso (with stretching arms) and the main person (without stretching arms) should be considered inferior detections. Depending on the IoU overlap, the NMS algorithm may suppress one of the predictions with lower confidence. This approach fails to give an “averaged” prediction that can capture the entire person object (represented by the solid line).
Owing to this attribute, NMS can pose more problems when we have an ensemble of object detection models.
Therefore, there arises a need to come up with a better approach that aims to obtain unified averaged predictions across multiple detection models.
Weighted Boxes Fusion: an Effective Post-Processing Approach
Owing to the downside of NMS discussed in the previous section; we can apply a more efficient approach called Weighted Boxes Fusion (WBF) to help achieve more robust averaged predictions across an ensemble of detection models.
The algorithm for Weighted Boxes Fusion was introduced in the paper: Weighted boxes fusion: Ensembling boxes from different object detection models.
The schematic illustration of WBF vs. NMS/Soft-NMS across an ensemble of predictions is shown below. The red box denotes the ground truth object, whereas the blue ones denote the predictions across various models.
The algorithm discussed in the paper is as follows:
- Each predicted box from each model is added to a single list B. The list is then sorted in decreasing order of the confidence scores C.
- We shall declare empty lists L and F for box clusters and fused boxes, respectively. Each position in the list L can contain a set of boxes (or a single box), which form a cluster; each position in F contains only one box, which is the fused box from the corresponding cluster in L.
- Next, we iterate through the predicted boxes in B and try to find a matching box in the list F. The matching criteria for a box bi in B to be in the same cluster is decided by the IoUthresh.
- If the IoU of box bi with the fused boxes in F is > IoUthresh, we add this box to L at the position pos corresponding to the matching box in F.
- Otherwise, we add bi to L and F as a new entry (or a new cluster).
- The box coordinates, and confidence score in Fpos are then recomputed using all T boxes accumulated in cluster Lpos.
- The fused confidence score is given by:
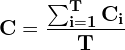
- The fused box coordinates are given by:
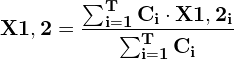
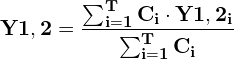
The coordinates of the fused box are the weighted sums of the coordinates of the boxes that form it, with the weights being the confidence scores for the corresponding boxes. Thus, boxes with larger confidence contribute more to the fused box coordinates than boxes with lower confidence.
- The fused confidence score is given by:
- Once all the boxes in B are processed, the confidence scores of the fused boxes in F are re-scaled using the equation below.
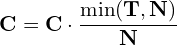
Here, N is the total number of models used for ensembling the predictions.
The equations discussed above may seem overwhelming, so let us illustrate them with an example.
Suppose at some instance, the list L has 3 clusters:
![$$L\ = \ [[b_1], [b_2\ b_3\ b_4], [b_5]]$$](data:image/svg+xml;nitro-empty-id=MTgxNzo2NTY=-1;base64,PHN2ZyB2aWV3Qm94PSIwIDAgMjI1IDIxIiB3aWR0aD0iMjI1IiBoZWlnaHQ9IjIxIiB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciPjwvc3ZnPg==)
The recomputed box coordinates and confidence scores for Clusters 1 and 3 will be the same as those in b1 and b5 since they are singletons.
Let the confidence scores for b2, b3, and b4 in cluster 2 are c2, c3, and c4, respectively.
Assume that their box coordinates are ![$\mathbf{[x2_{min}, y2_{min}, x2_{max}, y2_{max}]}$](data:image/svg+xml;nitro-empty-id=MTgyNTo1NjI=-1;base64,PHN2ZyB2aWV3Qm94PSIwIDAgMjUyIDIxIiB3aWR0aD0iMjUyIiBoZWlnaHQ9IjIxIiB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciPjwvc3ZnPg==)
, ![$\mathbf{[x3_{min}, y3_{min}, x3_{max}, y3_{max}]}$](data:image/svg+xml;nitro-empty-id=MTgyNToxMDg1-1;base64,PHN2ZyB2aWV3Qm94PSIwIDAgMjUyIDIxIiB3aWR0aD0iMjUyIiBoZWlnaHQ9IjIxIiB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciPjwvc3ZnPg==)
, and ![$\mathbf{[x4_{min}, y4_{min}, x4_{max}, y4_{max}]}$](data:image/svg+xml;nitro-empty-id=MTgyNToxNjEy-1;base64,PHN2ZyB2aWV3Qm94PSIwIDAgMjUyIDIxIiB3aWR0aD0iMjUyIiBoZWlnaHQ9IjIxIiB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciPjwvc3ZnPg==)
respectively.
The fused confidence C for cluster 2 is computed as:
(T=3 as there are 3 boxes in cluster 2)
The fused Xmin is computed as:
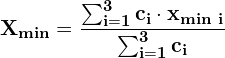
Similar calculations are followed for fused: Ymin, Xmax, and Ymax.
Code Explanation for Weighted Boxes Fusion and Non-Maximum Suppression
We shall use the ensemble-boxes package and the weighted_boxes_fusion utility function to compute the fused scores.
We will use the nms utility from torchvision.ops to perform NMS.
We have used 4 YOLOv8 models (small, medium, large, and extra-large) fine-tuned on the wheat-heads dataset available from the Global Wheat Detection Challenge, a very popular competition held at Kaggle in 2020, to demonstrate the prediction ensembling.
The samples used for inference are too taken from the same dataset.
We will maintain the following directory structure for the image samples and the models.
├── test-samples
│ ├── 348a992bb.jpg
│ ├── 51b3e36ab.jpg
│ ├── cc3532ff6.jpg
│ └── f5a1f0358.jpg
└── yolov8-global-wheat-models
├── yolov8_l_best.pt
├── yolov8_m_best.pt
├── yolov8_s_best.pt
└── yolov8_x_best.pt
We shall install the following dependencies before we start with our experiments.
!pip install ultralytics ensemble-boxes
We shall now initialize the directories for the sample images and the models.
SAMPLE_IMG_DIR = "test-samples"
MODELS_DIR = "yolov8-global-wheat-models"
Our next task is to create a mapping from Image ID (which is basically the filename) to its corresponding resolution (i.e., the height and width). The get_data_resolution utility maintains a dictionary mapping from the IDs to their resolutions. The image resolutions would be required later to scale the predictions before they can be passed to the weighted_boxes_fusion utility.
def get_data_resolution(image_dir_path, img_files):
image_res = dict()
for img_file in img_files:
img_filepath = os.path.join(image_dir_path, img_file)
image_id = img_file.strip().split(".")[0]
image = Image.open(img_filepath)
image_res[image_id] = image.size
return image_res
We shall next obtain the model predictions and maintain three separate dictionaries for the predicted bounding boxes, confidence scores, and class labels with the ImageIDs as keys. The get_predictions function achieves this.
def get_predictions(model, image_dir_path, image_filenames, conf_thres=0.25):
preds_scores = dict()
pred_boxes = dict()
pred_classes = dict()
for image_file in image_filenames:
img_filepath = os.path.join(image_dir_path, image_file)
image_id = image_file.strip().split(".")[0]
pred_results = model.predict(img_filepath, conf=conf_thres)[0].boxes.cpu()
preds_scores[image_id] = pred_results.conf.unsqueeze(dim=1).numpy()
pred_boxes[image_id] = pred_results.xyxy.numpy()
pred_classes[image_id] = pred_results.cls.int().unsqueeze(dim=1).numpy()
return preds_scores, pred_boxes, pred_classes
Recall that we have trained 4 YOLOv8 models: small(s), medium(m), large(l), and xtra large(x) on the wheat data. The predictions would be ensembled and filtered out later on.
We shall instantiate each of these models first by maintaining a dictionary model_dict.
model_dict = dict()
sample_img_files = os.listdir(SAMPLE_IMG_DIR)
data_res_dict = get_data_resolution(SAMPLE_IMG_DIR, sample_img_files)
ckpt_files = os.listdir(MODELS_DIR)
# Initialize Model Checkpoints.
for pt_file in ckpt_files:
model_dict["yolov8_"+pt_file.split("_")[1]] = YOLO(os.path.join(MODELS_DIR, pt_file))
We will now obtain the prediction data for each of the above-instantiated models and append them to lists pred_confs, pred_boxes, and pred_classes.
pred_confs = []
pred_boxes = []
pred_classes = []
for model_obj in model_dict.values():
confs_scores, box_preds, cls_preds = get_predictions(
model_obj,
SAMPLE_IMG_DIR,
sample_img_files)
pred_confs.append(confs_scores)
pred_boxes.append(box_preds)
pred_classes.append(cls_preds)
Perform Non-Maximum Suppression (NMS)
The perform_non_max_suppression utility is used to perform NMS across the model ensembles. Let us take a look at the function.
It takes the following arguments:
pred_confs_models: the list of predicted confidence scores across the models.pred_boxes_models: the list of predicted bounding box coordinates across the models.image_ids: the list of Image IDs.IOU_THRESH: The IoU or NMS threshold.FINAL_CONF_THRESH: The confidence threshold to further filter out the boxes after NMS.
def perform_non_max_suppression(
pred_confs_models,
pred_boxes_models,
image_ids,
IOU_THRESH,
FINAL_CONF_THRESH=None):
nms_boxes_dict = dict()
nms_scores_dict = dict()
for image_id in image_ids:
all_model_boxes = []
all_model_scores = []
for boxes, scores in zip(pred_boxes_models, pred_confs_models):
all_model_boxes.append(torch.from_numpy(boxes[image_id]))
all_model_scores.append(torch.from_numpy(scores[image_id]))
# Concatenate predicted bounding boxes and conf scores across all models.
all_model_boxes = torch.cat(all_model_boxes)
all_model_scores = torch.cat(all_model_scores).squeeze()
# Perform NMS on the predictions.
# The variable 'keep' returns the indices of predictions that are retained
# after NMS in decreasing order of conf. scores.
keep = nms(
boxes=all_model_boxes,
scores=all_model_scores,
iou_threshold=IOU_THRESH)
# Obtain the filtered boxes and scores after NMS.
boxes_retained = all_model_boxes[keep]
scores_retained = all_model_scores[keep]
# Further filter out boxes having scores > FINAL_CONF_THRESH.
final_scores_ids = torch.where(scores_retained > FINAL_CONF_THRESH)[0]
final_boxes = boxes_retained[final_scores_ids]
final_scores = scores_retained[final_scores_ids]
# Box coordinates in [xmin, ymin, width, height] format.
final_boxes = final_boxes.int()
final_boxes[:,2:] = final_boxes[:,2:] - final_boxes[:, :2]
# Append final_boxes and final_scores in dictionaries mapped with IMAGE_IDs.
nms_boxes_dict[image_id] = final_boxes.tolist()
nms_scores_dict[image_id] = torch.unsqueeze(final_scores, dim=-1).tolist()
return nms_boxes_dict, nms_scores_dict
- Lines 8-9 initialize dictionaries to store the final filtered boxes and scores after NMS with IDs as keys.
- Lines 13-14 maintain the lists for storing the predicted box coordinates and confidence scores across all 4 detection models for each image simultaneously. These lists are concatenated before they are passed to the
nmsutility function. - Lines 16-18 iterate through the predicted box coordinates and confidence scores across the models for each image and appends them to the previously initialized lists.
- Lines 27-30: The variable ‘keep’ returns the indices of predictions that are retained after NMS in decreasing order of confidence scores.
- Lines 33-34 obtain the filtered-out boxes and scores.
- Lines 37-40 further filter out the boxes based on
FINAL_CONF_THRESH - Line 44 converts the boxes in [xmin, ymin, width, height] format.
- Lines 47-48 convert the tensors to lists and append them to the dictionaries: nms_boxes_dict and nms_scores_dict, respectively.
The final predicted boxes and scores are stored in boxes_dict_nms and scores_dict_nms, respectively.
image_ids = list(data_res_dict.keys())
boxes_dict_nms, scores_dict_nms = perform_non_max_suppression(
pred_confs,
pred_boxes,
image_ids,
IOU_THRESH=0.50,
FINAL_CONF_THRESH=0.28)
Perform Weighted Boxes Fusion (WBF)
The weighted_boxes_fusion function accepts the box coordinates across the different models as lists in [xmin, ymin, xmax, ymax] in a normalized format.
The perform_weighted_boxes_fusion function accepts the confidence scores, bounding box coordinates, and class labels obtained in the previous section and returns the fused box coordinates (in [xmin, ymin, width, height] format) and confidence scores as dictionaries with ImageIds as keys.
Similar to the perform_non_max_suppression utility, the perform_weighted_boxes_fusion function takes the following arguments:
pred_confs_models: the list of predicted confidence scores across the models.pred_boxes_models: the list of predicted bounding box coordinates across the models.resolution_dict: a dictionary mapping from Image IDs to its corresponding shape.IOU_THRESH: The IoU threshold to filter out the predictions.CONF_THRESH: To exclude boxes with confidences lower than this threshold.FINAL_CONF_THRESH: The confidence threshold to further filter out the boxes after NMS.
def perform_weighted_boxes_fusion(
pred_confs_models,
pred_boxes_models,
pred_classes_models,
resolution_dict,
IOU_THRESH=0.5,
CONF_THRESH=None,
FINAL_CONF_THRESH=1e-3):
wbf_boxes_dict = dict()
wbf_scores_dict = dict()
for image_id, res in resolution_dict.items():
res_array = np.array([res[1], res[0], res[1], res[0]]) # [W, H, W, H]
all_model_boxes = []
all_model_scores = []
all_model_classes = []
for boxes, scores, classes in zip(pred_boxes_models, pred_confs_models, pred_classes_models):
# Normalize [xmin, ymin, xmax, ymax] in normalized form.
pred_boxes_norm = (boxes[image_id] / res_array).clip(min=0., max=1.)
scores_model = scores[image_id]
classes_model = classes[image_id]
all_model_boxes.append(pred_boxes_norm)
all_model_scores.append(scores_model)
all_model_classes.append(classes_model)
# Perform weighted box fusion.
boxes, scores, labels = weighted_boxes_fusion(
all_model_boxes,
all_model_scores,
all_model_classes,
weights=None,
iou_thr=IOU_THRESH,
skip_box_thr=CONF_THRESH)
# Further filter out boxes having scores > FINAL_CONF_THRESH.
final_scores_ids = np.where(scores > FINAL_CONF_THRESH)[0]
final_boxes = boxes[final_scores_ids]
final_scores = scores[final_scores_ids]
# Box coordinates in [xmin, ymin, xmax, ymax] in de-normalized form.
final_boxes = (final_boxes*res_array).clip(min=[0.,0.,0.,0.],
max=[res[1]-1, res[0]-1, res[1]-1, res[0]-1])
final_boxes = final_boxes.astype("int")
# Box coordinates in [xmin, ymin, width, height] in de-normalized form.
final_boxes[:,2:] = final_boxes[:,2:] - final_boxes[:, :2]
wbf_boxes_dict[image_id] = final_boxes.tolist()
wbf_scores_dict[image_id] = np.expand_dims(np.round(final_scores, 5), axis=-1).tolist()
return wbf_boxes_dict, wbf_scores_dict
- Lines 10-11 initialize dictionaries to store the final filtered boxes and scores after WBF with IDs as keys.
- Lines 17-19 maintain the lists for storing the predicted box coordinates and confidence scores and the class labels across all 4 detection models for each image simultaneously.
- Lines 21-30 iterate through the predicted box coordinates, confidence scores, and class labels across the models, each image at a time. The predicted boxes are then normalized in the range [0,1]. Finally, the boxes, scores, and labels are appended to the previously initialized lists.
- Line 33-39: returns the filtered-out boxes, scores, and labels after performing WBF.
- Lines 43-46 further filter out the boxes and scores based on FINAL_CONF_THRESH
- Lines 49-50: The final boxes are de-normalized into absolute coordinates.
- Line 55 converts the boxes in [xmin, ymin, width, height] format.
- Lines 57-58 convert the numpy arrays to lists and append them to the dictionaries: wbf_boxes_dict and wbf_scores_dict, respectively.
The final predicted boxes and scores are stored in boxes_dict_wbf and scores_dict_wbf, respectively.
boxes_dict_wbf, scores_dict_wbf = perform_weighted_boxes_fusion(
pred_confs,
pred_boxes,
pred_classes,
data_res_dict,
IOU_THRESH=0.50,
CONF_THRESH=0.32,
FINAL_CONF_THRESH=0.28)
Visualizations across Weighted Boxes Fusion and Non-Maximum Suppression
The draw_bbox_conf utility plots the bounding boxes and the confidence scores on the corresponding image.
def draw_bbox_conf(image, boxes, scores, class_name, color=(255, 0, 0), thickness=-1):
overlay = image.copy()
font_size = 0.25 + 0.07 * min(overlay.shape[:2]) / 100
font_size = max(font_size, 0.5)
font_size = min(font_size, 0.8)
text_offset = 7
for box, score in zip(boxes, scores):
xmin = box[0]
ymin = box[1]
xmax = box[0]+box[2]
ymax = box[1]+box[3]
overlay = cv2.rectangle(overlay,
(xmin, ymin),
(xmax, ymax),
color,
thickness)
display_text = f"{class_name}: {score[0]:.2f}"
(text_width, text_height), _ = cv2.getTextSize(display_text,
cv2.FONT_HERSHEY_SIMPLEX,
font_size, 2)
cv2.rectangle(overlay,
(xmin, ymin),
(xmin + text_width + text_offset,
ymin - text_height - int(15 * font_size)),
color, thickness=-1)
overlay = cv2.putText(
overlay,
display_text,
(xmin + text_offset, ymin - int(10 * font_size)),
cv2.FONT_HERSHEY_SIMPLEX,
font_size,
(255, 255, 255),
2, lineType=cv2.LINE_AA,
)
return cv2.addWeighted(overlay, 0.75, image, 0.25, 0)
The following subplots show the inference results for NMS.
The following subplots show the inference results for WBF.
Let us zoom in on a few instances and observe the results across NMS and WBF without the confidence scores.
The 1st column shows the results from traditional NMS, while the 2nd column shows the results with WBF. For all these instances, the WBF algorithm was able to generate averaged localization predictions.
Furthermore, we performed submissions for both of these approaches in the Global Wheat Competition Challenge on Kaggle. This competition is evaluated on the Mean Average Precision (mAP) at different IoU thresholds. The threshold values range from 0.5 to 0.75 with a step size of 0.05. The following are the results.
Kaggle Submission Scores for NMS:
Kaggle Submission Scores for WBF:
The two numbers denote the Private and Public Leaderboard scores on Kaggle, respectively. WBF was able to produce a significant improvement in the results.
This might be attributed to the relatively more false positives with traditional NMS than WBF, resulting in decreased precision for NMS.
Conclusion
As we wrap up this engaging article, we have effectively unraveled the crucial role of Weighted Boxes Fusion (WBF) as an ingenious post-processing measure within object detection, chiefly when applied to a diverse ensemble of detection models. Our exploration has shed light on the inherent limitations of the traditional Non-Maximum Suppression methodology for multi-model predictions, paving the way for WBF’s effectiveness in assuaging these issues by offering a cohesive, averaged prediction across different object instances.
Furthermore, we have highlighted the transformative potential of WBF in drastically boosting submission scores for grand-scale detection contests hosted on renowned platforms like Kaggle.
