Non Maximum Suppression: Theory and Implementation in PyTorch

Non Maximum Suppression (NMS) is a technique used in numerous computer vision tasks. It is a class of algorithms to select one entity (e.g., bounding boxes) out of many overlapping entities. We can choose the selection criteria to arrive at the desired results. The criteria are most commonly some form of probability number and some form of overlap measure (e.g. Intersection over Union).

This post will go over how it works and implement it in Python using the PyTorch framework. So without further ado, let us get started 🙂

Why we need it ?

Before we discuss how NMS works, we must try to answer why we need it first.

Most object detection algorithms use NMS to whittle down many detected bounding boxes to only a few. At the most basic level, most object detectors do some form of windowing. Thousands of windows (anchors) of various sizes and shapes are generated.

These windows supposedly contain only one object, and a classifier is used to obtain a probability/score for each class. Once the detector outputs a large number of bounding boxes, it is necessary to filter out the best ones. NMS is the most commonly used algorithm for this task.

Now that we know why we need it let us dive into the explanation of how it works.

Intersection Over Union (IoU)

Before we go ahead, I would like to discuss this one concept that we will be using in the following sections i.e. Intersection Over Union or IoU in short.

Jaccard index,

The Intersection over Union (IoU) metric, also referred to as the Jaccard index, is essentially a method used usually to quantify the percent overlap between the ground truth BBox (Bounding Box) and the prediction BBox. However, in NMS, we find IoU between two predictions BBoxes instead.

IoU in mathematical terms can be represented by the following expression,

Intersection Over Union(IoU) = (Target ∩ Prediction) / (Target U Prediction)

In our case using BBoxes, it can be modified to,

IOU(Box1, Box2) = Intersection_Size(Box1, Box2) / Union_Size(Box1, Box2)

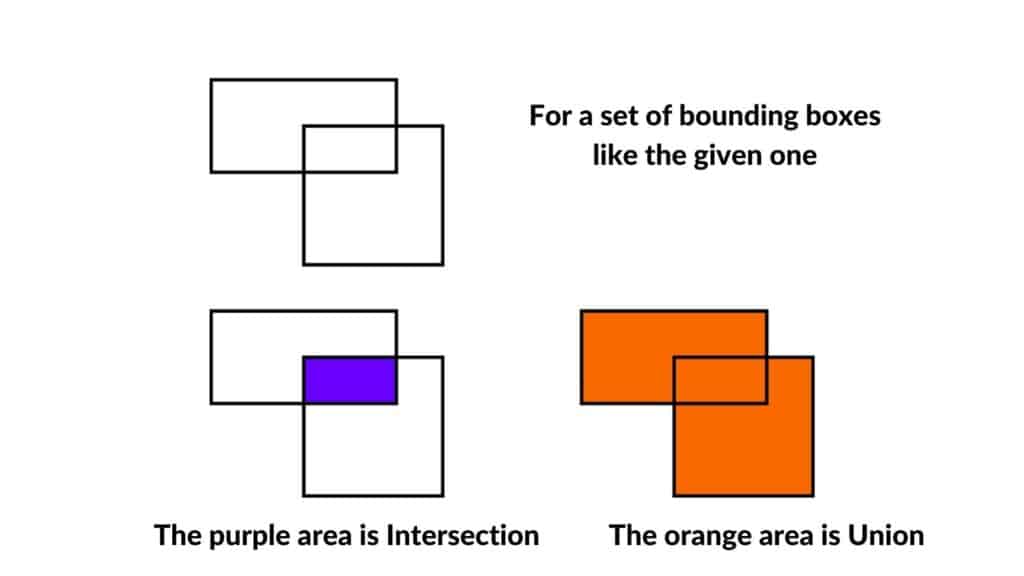
Consider the the two BBoxes in the following figure,

Their union area is the orange area, and their intersection area is the purple area. So the IoU can be calculated by dividing the purple area by the orange area.

Implementation of IoU in Python

Let us implement this in Python so that we can use it in the later sections. Consider two BBoxes, namely

Box1 having lower left coordinates as (x1,y1) and upper right coordinates as (a1,b1).

Similarly, there is another BBox, called Box2 having coordinates (x2,y2) and (a2,b2).

We find their intersection box that has coordinates (xx,yy) and (aa,bb).

We then use the expression discussed above to find IoU.

# find the area for the box1 (x1,y1) (a1,b1)
area1 = (a1-x1)*(b1-y1);

# find the area for the box2 (x2,y2) (a2,b2)
area2 = (a2-x2)*(b2-y2);

# Now we need to find the intersection box
# to do that, find the largest (x, y) coordinates 
# for the start of the intersection bounding box and 
# the smallest (x, y) coordinates for the 
# end of the intersection bounding box
xx = max(x1, x2)
yy = max(y1, y2)
aa = min(a1, a2)
bb = min(b1, b2)

# So the intersection BBox has the coordinates (xx,yy) (aa,bb)
# compute the width and height of the intersection bounding box
w = max(0, aa - xx)
h = max(0, bb - yy)

# find the intersection area
intersection_area = w*h

# find the union area of both the boxes
union_area = area1 + area2 - intersection_area

# compute the ratio of overlap between the computed
# bounding box and the bounding box in the area list
IoU = intersection_area / union_area

Click here to download the source code to this post

The NMS Algorithm

Let us get to the nitty-gritty of this post, the actual algorithm. I will divide this into three parts, what we need as input, what we get after applying the algorithm and the actual algorithm itself.

Input

We get a list P of prediction BBoxes of the form (x1,y1,x2,y2,c), where (x1,y1) and (x2,y2) are the ends of the BBox and c is the predicted confidence score of the model. We also get overlap threshold IoU thresh_iou.

Output

We return a list keep of filtered prediction BBoxes.

Algorithm

Step 1 : Select the prediction S with highest confidence score and remove it from P and add it to the final prediction list keep. (keep is empty initially).

Step 2 : Now compare this prediction S with all the predictions present in P. Calculate the IoU of this prediction S with every other predictions in P. If the IoU is greater than the threshold thresh_iou for any prediction T present in P, remove prediction T from P.

Step 3 : If there are still predictions left in P, then go to Step 1 again, else return the list keep containing the filtered predictions.

In layman terms, we select the predictions with the maximum confidence and suppress all the other predictions having overlap with the selected predictions greater than a threshold. In other words, we take the maximum and suppress the non-maximum ones, hence the name non-maximum suppression.

If you observe the algorithm above, the whole filtering process depends on a single threshold value thresh_iou. So selection of threshold value is vital for the performance of the model. Usually, we take its value as 0.5, but it depends on the experiment you are doing.As discussed in the NMS algorithm above, we extract the BBox of highest confidence score and remove it from P.

Now that we have a good grasp of how NMS works, let us implement it in PyTorch so that you can use it in your future Object Detection pipelines 🙂

Implementation of NMS in PyTorch

Let us begin with the fun part.

We define the function that takes in a list of prediction boxes along with their confidence score and a thresh_iou.

Define the function

def nms_pytorch(P : torch.tensor ,thresh_iou : float):
    """
    Apply non-maximum suppression to avoid detecting too many
    overlapping bounding boxes for a given object.
    Args:
        boxes: (tensor) The location preds for the image 
            along with the class predscores, Shape: [num_boxes,5].
        thresh_iou: (float) The overlap thresh for suppressing 
            unnecessary boxes.
    Returns:
        A list of filtered boxes, Shape: [ , 5]
    """

    # we extract coordinates for every 
    # prediction box present in P
    x1 = P[:, 0]
    y1 = P[:, 1]
    x2 = P[:, 2]
    y2 = P[:, 3]

When I say coordinate (x1,y1), I refer to the lower left coordinate of the BBox and (x2,y2) refers to the upper right coordinate of the BBox.

We extract all the x1 coordinates using simple slicing , P[ : , 0]. Similarly we extract the x2, y1 and y2 coordinates as well.

    # we extract the confidence scores as well
    scores = P[:, 4]

We also extract the confidence scores in scores.

    # calculate area of every block in P
    areas = (x2 - x1) * (y2 - y1)
    
    # sort the prediction boxes in P
    # according to their confidence scores
    order = scores.argsort()

    # initialise an empty list for 
    # filtered prediction boxes
    keep = []

We find the area of every BBox in P and store in areas. We also initialise an empty list keep as discussed above to store the filtered predictions.

Now we argsort(Argument Sort) the list scores, i.e. order will contain the respective indices of the scores if it had been sorted.

For example, if scores = [0.7, 0.3, 0.6], then order = scores.argsort() = [1, 2, 0].

So now we have the indices of every BBox in P sorted according to their confidence scores.

Step 1 :

Finding BBox S with highest score

    while len(order) > 0:
        
        # Step 1
        # extract the index of the 
        # prediction with highest score
        # we call this prediction S
        idx = order[-1]

        # push S in filtered predictions list
        keep.append(P[idx])

        # remove S from P
        order = order[:-1]

As discussed in the NMS algorithm above, we extract the BBox with the highest confidence score and remove it from P. We select S using idx = order[-1] and then push this prediction in filtered box list keep. (So here, S is actually P[idx])

        # select coordinates of BBoxes according to 
        # the indices in order
        xx1 = torch.index_select(x1,dim = 0, index = order)
        xx2 = torch.index_select(x2,dim = 0, index = order)
        yy1 = torch.index_select(y1,dim = 0, index = order)
        yy2 = torch.index_select(y2,dim = 0, index = order)

Next we extract all the x1 coordinates according to the indices present in order.

For example, if order = [2, 0, 1] and x1 = [2.0, 7.0, 4.0], then xx1 = [4.0, 2.0, 7.0].

Torch.index_select selects elements from a input tensor according to an index list. In our case index = order and input = x1.

Similarly we do it for x2,y1 and y2.

Step 2 :

Finding intersection BBoxes between S and all predictions left in P

        # Step 2
        # find the coordinates of the intersection boxes
        xx1 = torch.max(xx1, x1[idx])
        yy1 = torch.max(yy1, y1[idx])
        xx2 = torch.min(xx2, x2[idx])
        yy2 = torch.min(yy2, y2[idx])

        # find height and width of the intersection boxes
        w = xx2 - xx1
        h = yy2 - yy1
        
        # take max with 0.0 to avoid negative w and h
        # due to non-overlapping boxes
        w = torch.clamp(w, min=0.0)
        h = torch.clamp(h, min=0.0)

Next, we find intersection bounding box of the selected prediction S = P[idx] with all other predictions left in P.

A thing to note is that(xx1,yy1) is the lower left corner of intersection BBox and(xx2,yy2)is the upper right corner of intersection BBox

Since to find the xx1 coordinate of the intersection BBox of the selected prediction S with any prediction T in P, we do xx1 = max(S.x1, T.x1). We do the same thing with this line, xx1 = torch.max(xx1, x1[idx])

x1[idx] is actually P.x1 since idx is the index of the current selected prediction S in P

Similarly, we find xx2, yy1 and yy2 and obtain intersection box coordinates of all the boxes present in P with the selected prediction S.

Next we find width w and height h of every intersection box and take a max with 0.0 to avoid negative w and h due to non-overlapping BBoxes.

Finding IoU between S and all other BBox left in P

        # find the intersection area
        inter = w*h

        # find the areas of BBoxes according the indices in order
        rem_areas = torch.index_select(areas, dim = 0, index = order) 

        # find the union of every prediction T in P
        # with the prediction S
        # Note that areas[idx] represents area of S
        union = (rem_areas - inter) + areas[idx]
        
        # find the IoU of every prediction in P with S
        IoU = inter / union

Now we find the intersection area inter of all intersection boxes. We get the areas of the BBoxes according to the indices present in order using torch.index_select, and then calculate union, which contains union area of all the BBoxes present in P with S.

union = (rem_areas - inter) + areas[idx]

First, subtract the intersection area from all boxes in P
Then, add the area of S, which adds back:
– the intersection area
– plus the extra area not present in intersection of S and T, but present in S.

Hence we have calculated the union of S and BBoxes T in P.

Next we find the IoU by simply dividing inter by union.

Filtering out BBox having IoU overlap with S greater than the threshold thresh_iou

        # keep the boxes with IoU less than thresh_iou
        mask = IoU < thresh_iou
        order = order[mask]
        
        # Step 3, check if there are still elements in P
    
    return keep

Now we need to eliminate all such BBoxes T in P having IoU >= thresh_iou. To achieve this, we create a mask using the criteria which elements in IoU have a value less than thresh_iou as those are the values we want to keep.

For example, if IoU = [0.4, 0.6, 0.3] and thresh_iou = 0.5, then mask = IoU < thresh_iou will result in mask = [True, False, True]. If we then apply mask over order, we get the list only with elements where corresponding element in mask was True.

For example, if score = [1, 0, 2] and mask = [True, False, True], then score[mask] = [1, 2].

So in this way we keep only those predictions whose IoU with the current prediction S is less than the thresh_iou and remove all those with greater than threshold.

Step 3 :

Putting it together

We repeat this loop until P or, in our case, order is not empty. We go out of the loop. We simply return keep that stored our filtered predictions.

Let us use a simple example to test out nms_pytorch function. Notice below that P is a tensor containing tensors of the form (x,y, a,b,c). We discussed this previously in the input section of the NMS algorithm. So if we put everything together, our NMS function looks like below:

def nms_pytorch(P : torch.tensor ,thresh_iou : float):
    """
    Apply non-maximum suppression to avoid detecting too many
    overlapping bounding boxes for a given object.
    Args:
        boxes: (tensor) The location preds for the image 
            along with the class predscores, Shape: [num_boxes,5].
        thresh_iou: (float) The overlap thresh for suppressing unnecessary boxes.
    Returns:
        A list of filtered boxes, Shape: [ , 5]
    """

    # we extract coordinates for every 
    # prediction box present in P
    x1 = P[:, 0]
    y1 = P[:, 1]
    x2 = P[:, 2]
    y2 = P[:, 3]

    # we extract the confidence scores as well
    scores = P[:, 4]

    # calculate area of every block in P
    areas = (x2 - x1) * (y2 - y1)
    
    # sort the prediction boxes in P
    # according to their confidence scores
    order = scores.argsort()

    # initialise an empty list for 
    # filtered prediction boxes
    keep = []
    

    while len(order) > 0:
        
        # extract the index of the 
        # prediction with highest score
        # we call this prediction S
        idx = order[-1]

        # push S in filtered predictions list
        keep.append(P[idx])

        # remove S from P
        order = order[:-1]

        # sanity check
        if len(order) == 0:
            break
        
        # select coordinates of BBoxes according to 
        # the indices in order
        xx1 = torch.index_select(x1,dim = 0, index = order)
        xx2 = torch.index_select(x2,dim = 0, index = order)
        yy1 = torch.index_select(y1,dim = 0, index = order)
        yy2 = torch.index_select(y2,dim = 0, index = order)

        # find the coordinates of the intersection boxes
        xx1 = torch.max(xx1, x1[idx])
        yy1 = torch.max(yy1, y1[idx])
        xx2 = torch.min(xx2, x2[idx])
        yy2 = torch.min(yy2, y2[idx])

        # find height and width of the intersection boxes
        w = xx2 - xx1
        h = yy2 - yy1
        
        # take max with 0.0 to avoid negative w and h
        # due to non-overlapping boxes
        w = torch.clamp(w, min=0.0)
        h = torch.clamp(h, min=0.0)

        # find the intersection area
        inter = w*h

        # find the areas of BBoxes according the indices in order
        rem_areas = torch.index_select(areas, dim = 0, index = order) 

        # find the union of every prediction T in P
        # with the prediction S
        # Note that areas[idx] represents area of S
        union = (rem_areas - inter) + areas[idx]
        
        # find the IoU of every prediction in P with S
        IoU = inter / union

        # keep the boxes with IoU less than thresh_iou
        mask = IoU < thresh_iou
        order = order[mask]
    
    return keep

Testing our NMS function

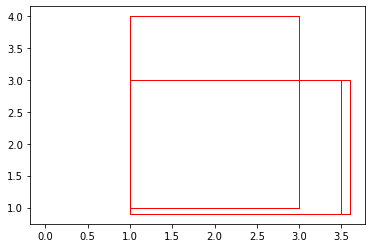
Let us use a very simple example to test out nms_pytorch function. Notice below that P is a tensor containing tensors of the form (x,y,a,b,c) as was discussed above in the input section of NMS algorithm.

# Let P be the following
P = torch.tensor([
    [1, 1, 3, 3, 0.95],
    [1, 1, 3, 4, 0.93],
    [1, 0.9, 3.6, 3, 0.98],
    [1, 0.9, 3.5, 3, 0.97]
])

If we plot prediction boxes in P, we get a figure like this.

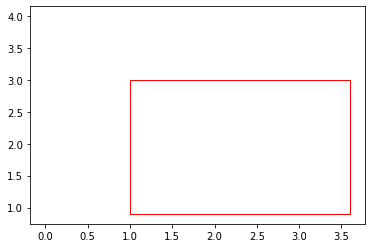
Now we run our nms_pytorch function with thresh_iou as 0.5.

filtered_boxes = nms_pytorch(P,0.5)

We get one filtered box and if we plot that, it will look like below.

So all the other extra overlapping boxes have been cleared out and we get a nice and clean prediction.

Now, lets’ try with IOU of 0.8.

filtered_boxes = nms_pytorch(P,0.8)

The following is the result that we get:

This time we have two boxes in the final plot. The reason is that this time the IoU was 0.8. And any box that has an IoU of less than 0.8 with the highest confidence box will not be suppressed and will be treated as a separate valid bounding box.

This is a very simple example. However, in this post, we have used an image with prediction boxes on it predicted by an actual Resnet model. If we look at the image below without applying NMS, there a lot of overlapping BBoxes (especially around the face of Fez, the rightmost guy with a light green shirt 🙂 )

I have provided the labels.txt containing all the prediction boxes in the code provided with this post. It also the contains the sample image as well as a function that shows the image before and after applying NMS algorithm. Make sure you check that out 🙂

Now if we apply our nms_pytorch function, we get the following image.

Woah !! That’s a pretty big difference. Looks like the NMS removed all the overlapping predictions and we got a very clean looking final prediction.

Outro

Congratulations on making it this far. That was a lot to cover, so I will recap it for you guys:

1. We learned what NMS is? And why is it used in object detection pipelines?
2. We learned about Intersection Over Union as a metric to quantify percent overlap between two BBoxes.
3. We got to know how NMS works and implemented it in PyTorch.
4. We tested it out on an example image and saw a massive difference between the prediction boxes in the images before and after applying NMS.

I have discussed the Vanilla NMS that is being used in a lot of computer vision pipelines currently. However, there are some problems with it that recent researches on NMS aim to fix. One of the solutions is Soft NMS algorithm. If you are interested in reading about this I recommend that you check out this research paper Soft-NMS.

So there you have it, your own implemented NMS in PyTorch that you can use in your deep learning pipelines.

That’s it from my side. I hope you enjoyed reading this. If there any questions, leave a comment below and I will try to answer them as soon as possible.

Until next time 🙂

References

[1] https://medium.com/@whatdhack/reflections-on-non-maximum-suppression-nms-d2fce148ef0a

[2] https://www.jeremyjordan.me/evaluating-image-segmentation-models/

[3] https://github.com/rbgirshick/fast-rcnn/blob/master/lib/utils/nms.py

[4] https://medium.com/koderunners/intersection-over-union-516a3950269c