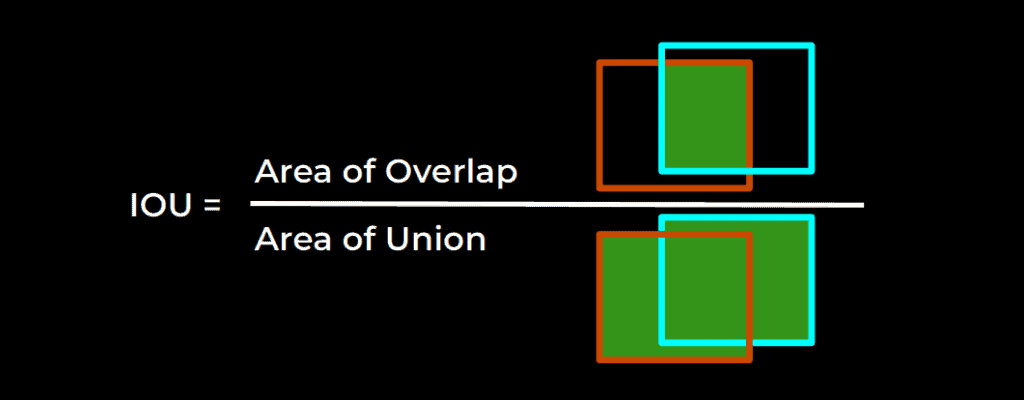
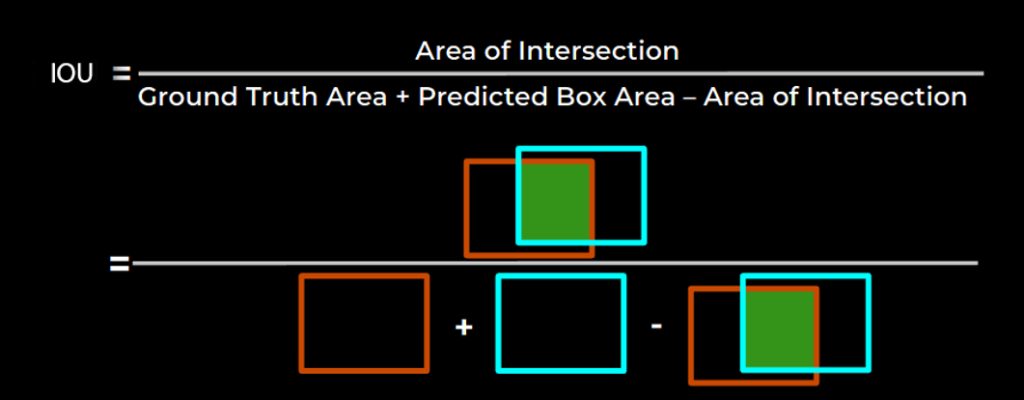
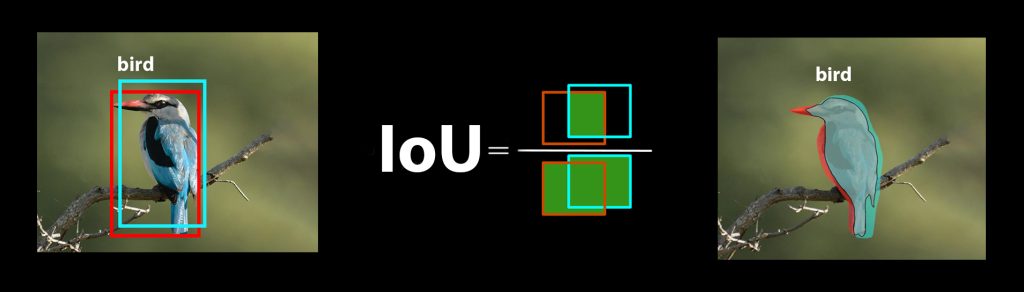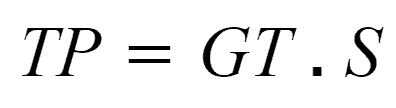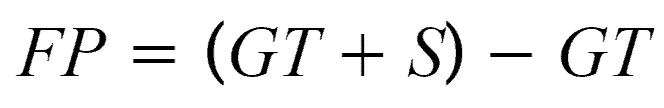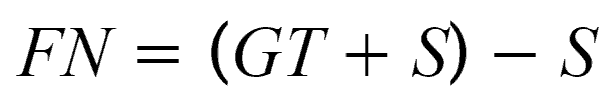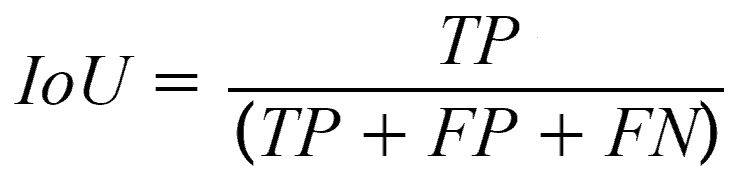Intersection over Union (IoU) in Object Detection & Segmentation

Intersection Over Union (IoU) is a number that quantifies the degree of overlap between two boxes. In the case of object detection and segmentation, IoU evaluates the overlap of the Ground Truth and Prediction region.

If you are a computer vision practitioner or even an enthusiast, you must have come across the term very often. It is the first checkpoint for evaluating the accuracy of a model. In simple terms, it’s a metric that helps us measure the correctness of a prediction.

1. Intersection over Union (IoU) in Object Detection
   1. Observations
   2. Designing IoU Metric for Object Detection
   3. Qualitative Analysis of Predictions
2. Intersection over Union (IoU) in Image Segmentation
3. A sample object detection example
4. Implementing IoU using NumPy
5. Implementing IoU using the built-in function box_iou in PyTorch
6. Implementing IoU manually using PyTorch
7. Conclusion

Intersection over Union in Object Detection

Let’s go through the following example to understand how IoU is calculated. Let three models- A, B, and C- be trained to predict birds. We pass an image through the models where we already know the Ground Truth (marked in red). The image below shows predictions of the models (marked in cyan).

1.1 Observations

• It is clear that the predicted box of Model A has more overlap with the Ground Truth as compared to Model B.
• However, Model C has an even higher overlap with the ground truth. But it also has a high overlap with the background.
• So from models B and C, it is clear that a metric based on only overlap is not a fair one as we should also account for localization accuracy. It is not just about matching the Ground Truth but how closely the prediction matches it. 
• Therefore, we need a metric that will penalize the metric whenever,
  • The prediction fails to predict the area inside the Ground Truth.
  • The prediction overflows the Ground Truth.

Keeping the above in mind, the IoU metric has been designed.

100K+ Learners
3 Hours of Learning

Join Free OpenCV Bootcamp

15K+ Learners
3 Hours of Learning

Join Free TensorFlow Bootcamp

10K+ Learners
8 Hours of Learning

Join Free PyTorch Bootcamp

View all AI Free Courses

1.2 Designing Intersection over Union metric for Object Detection

It is the ratio of the overlap area to the combined area of prediction and ground truth. The numerator will be lesser as the prediction fails to predict the area inside the ground truth. If the area of the predicted box is higher, the denominator will be higher, making the IoU lower. 

IoU values range from 0 to 1. Where 0 means no overlap and 1 means perfect overlap.

Looking closely, we are adding the area of the intersection twice in the denominator. So actually, we calculate IoU as shown in the illustration below.

1.3 Qualitative Analysis of Predictions

With the help of the IoU threshold, we can decide whether the prediction is True Positive(TP), False Positive(FP), or False Negative(FN). The example below shows predictions with the IoU threshold ɑ set at 0.5.

The decision of making a detection as True Positive or False Positive completely depends on the requirement.

• The first prediction is True Positive as the IoU threshold is 0.5.
• If we set the threshold at 0.97, it becomes a False Positive.
• Similarly, the second prediction shown above is False Positive due to the threshold but can be True Positive if we set the threshold at 0.20.
• Theoretically, the third prediction can also be True Positive, given that we lower the threshold all the way to 0.

Intersection over Union in Image Segmentation

IoU in object detection is a helper metric. However, in image segmentation, IoU is the primary metric to evaluate model accuracy.

In the case of Image Segmentation, the area is not necessarily rectangular. It can have any regular or irregular shape. That means the predictions are segmentation masks and not bounding boxes. Therefore, pixel-by-pixel analysis is done here. Moreover, the definition of TP, FP, and FN is slightly different as it is not based on a predefined threshold.

(a) True Positive: The area of intersection between Ground Truth(GT) and segmentation mask(S). Mathematically, this is logical AND operation of GT and S i.e., 

(b) False Positive: The predicted area outside the Ground Truth. This is the logical OR of GT and segmentation minus GT. 

(c) False Negative: Number of pixels in the Ground Truth area that the model failed to predict. This is the logical OR of GT and segmentation minus S.

We know from Object Detection that IoU is the ratio of the intersected area to the combined area of prediction and ground truth. Since the values of TP, FP, and FN are nothing but areas or number of pixels; we can write IoU as follows.

Note that we have already provided colab notebooks for PyTorch and Numpy versions in the code download section. Therefore, no need to install dependencies manually. However, if you use them locally, install PyTorch from the official source.

A Sample Object Detection Example

In the image above, the blue bounding box is the detected object. Given that the Ground Truth is known (shown in red), let us see how to implement IoU calculation using NumPy and PyTorch. We will see the available in-built function and define manual functions as well.

In the order of top left to bottom right corner, the coordinates are,

In practice, the predictions are obtained from model inference.

Click here to download the source code to this post

Implementing Intersection over Union using NumPy

Now that we know how IoU is calculated in theory let us define a function to calculate IoU with our data, i.e., coordinates of the Ground Truth and Prediction.

(a). Import Dependencies for IoU

import numpy as np
np.__version__

(b). Defining a Function to Calculate IoU

Here, we find the coordinates of the bounding box surrounding the intersection area. Then subtract the area of intersection from the sum of the area of Ground Truth and Prediction. We add 1 while calculating height and width to counter zero division errors. Theoretically, it is possible to add an infinitesimally small positive value, say 0.0001. However, images are discrete. The minimum possible dimension of an image is 1×1. Therefore, we have to add 1.

def get_iou(ground_truth, pred):
    # coordinates of the area of intersection.
    ix1 = np.maximum(ground_truth[0], pred[0])
    iy1 = np.maximum(ground_truth[1], pred[1])
    ix2 = np.minimum(ground_truth[2], pred[2])
    iy2 = np.minimum(ground_truth[3], pred[3])
    
    # Intersection height and width.
    i_height = np.maximum(iy2 - iy1 + 1, np.array(0.))
    i_width = np.maximum(ix2 - ix1 + 1, np.array(0.))
    
    area_of_intersection = i_height * i_width
    
    # Ground Truth dimensions.
    gt_height = ground_truth[3] - ground_truth[1] + 1
    gt_width = ground_truth[2] - ground_truth[0] + 1
    
    # Prediction dimensions.
    pd_height = pred[3] - pred[1] + 1
    pd_width = pred[2] - pred[0] + 1
    
    area_of_union = gt_height * gt_width + pd_height * pd_width - area_of_intersection
    
    iou = area_of_intersection / area_of_union
    
    return iou

(c). Bounding Box Coordinates

ground_truth_bbox = np.array([1202, 123, 1650, 868], dtype=np.float32)

prediction_bbox = np.array([1162.0001, 92.0021, 1619.9832, 694.0033], dtype=np.float32)

(d). Get IoU Value

iou = get_iou(ground_truth_bbox, prediction_bbox)
print('IOU: ', iou)

Output

IOU:  0.6441399913136432

PyTorch Built-In Function for IoU

Pytorch already has a built-in function box_iou [1] to calculate IoU. Documentation in the Reference section. It takes the set of bounding boxes as inputs and returns an IoU tensor.

# Import dependencies.
import torch
from torchvision import ops

# Bounding box coordinates.
ground_truth_bbox = torch.tensor([[1202, 123, 1650, 868]], dtype=torch.float)
prediction_bbox = torch.tensor([[1162.0001, 92.0021, 1619.9832, 694.0033]], dtype=torch.float)

# Get iou.
iou = ops.box_iou(ground_truth_bbox, prediction_bbox)
print('IOU : ', iou.numpy()[0][0])

Output

IOU : 0.6436676

Implementing IoU by defining a function in PyTorch

The code flow is similar to the NumPy implementation that we have done above.

(a). Import Dependencies

import torch
torch.__version__

(b). Function to Calculate IoU

def get_iou_torch(ground_truth, pred):
    # Coordinates of the area of intersection.
    ix1 = torch.max(ground_truth[0][0], pred[0][0])
    iy1 = torch.max(ground_truth[0][1], pred[0][1])
    ix2 = torch.min(ground_truth[0][2], pred[0][2])
    iy2 = torch.min(ground_truth[0][3], pred[0][3])
   
    # Intersection height and width.
    i_height = torch.max(iy2 - iy1 + 1, torch.tensor(0.))
    i_width = torch.max(ix2 - ix1 + 1, torch.tensor(0.))
   
    area_of_intersection = i_height * i_width
   
    # Ground Truth dimensions.
    gt_height = ground_truth[0][3] - ground_truth[0][1] + 1
    gt_width = ground_truth[0][2] - ground_truth[0][0] + 1
   
    # Prediction dimensions.
    pd_height = pred[0][3] - pred[0][1] + 1
    pd_width = pred[0][2] - pred[0][0] + 1
   
    area_of_union = gt_height * gt_width + pd_height * pd_width - area_of_intersection
   
    iou = area_of_intersection / area_of_union
   
    return iou

(c). Bounding Box Coordinates

The prediction bounding box is usually obtained while performing model inference. We are defining it manually here for the sake of simplicity.

ground_truth_bbox = torch.tensor([[1202, 123, 1650, 868]], dtype=torch.float)

prediction_bbox = torch.tensor([[1162.0001, 92.0021, 1619.9832, 694.0033]], dtype=torch.float)

(d). Get IoU Value

iou_val = get_iou_torch(ground_truth_bbox, prediction_bbox)
print('IOU : ', iou_val.numpy()[0][0])

Output

IOU :  0.64413995

We can see that the output varies slightly. This error is introduced for adding 1 to counter zero division error. In practice, values are clamped to a Min-Max range. Here, let’s keep it as it is for the sake of simplicity. You can also look at the source code [2] for a better understanding.

Conclusion

So that’s all about Intersection over Union or Jaccard Index. In this blog post, we discussed the basics of IoU and why it is needed. You also learned the implementation of IoU using NumPy and PyTorch. It should be noted that IoU in object detection does not have the same meaning in segmentation.

In object detection, IoU does not calculate the accuracy of a model directly. Rather, it is a helper metric that evaluates the degree of overlap between ground truth and the prediction.

We have Average Precision (AP) and Mean Average Precision (mAP) metrics for evaluating model accuracy. When we see mAP@0.5, mAP@0.75, etc. These are essentially mAP values calculated at IOU thresholds 0.5 and 0.75 respectively. We will discuss more on mAP in a separate blog post.

Must Read Articles

References