Have you ever wondered how robots navigate autonomously, grasp different objects, or avoid collisions while moving? Using stereo vision-based depth estimation is a common method used for such applications. In this post, we discuss classical methods for stereo matching and for depth perception. We explain depth perception using a stereo camera and OpenCV. We share the code in Python and C++ for hands-on experience.
This post is part of our series on Introduction to Spatial AI, which consists of the following articles :
- Introduction to Epipolar Geometry and Stereo Vision
- Making A Low-Cost Stereo Camera Using OpenCV
- Depth Estimation Using Stereo Camera and OpenCV
- More to come
Following and understanding this post and its content requires understanding the basics involved. If you are not already familiar with it, here is the list of prerequisite posts for you to read before proceeding further:
For tasks such as grasping objects and avoiding collision while moving, the robots need to perceive the world in 3D space. Following is the demonstration of an obstacle avoidance robot, which uses stereo vision-based depth estimation to perceive the world in 3D.
Recap of learning from the first two posts of this series
In the epipolar geometry & stereo vision article of the Introduction to spatial AI series, we discussed two essential requirements to estimate the depth (the 3D structure) of a given scene: point correspondence and the cameras’ relative position.
A quick recap: corresponding points are pixels of different images that are projections of the same 3D point. Finding point correspondence for all the 3D points captured in both the images of a stereo image pair gives us dense correspondence, which can be used to find a dense depth map and perceive the 3D world.
We observed that it is often challenging to find dense correspondence and realized the beauty and efficiency of epipolar geometry in reducing the search space for point correspondence. We also discussed how having parallel epipolar lines further simplifies the problem, as the corresponding points relate by a horizontal displacement. This displacement is called disparity.
In the making a low cost stereo camera using OpenCV article of the Introduction to spatial AI series, we created a custom low- cost stereo camera. We also discussed stereo rectification and calibration. Stereo rectification and calibration are performed to make the epipolar lines horizontal. These calculations make it easy to find dense correspondence.
This post discusses Block Matching and Semi-Global Block Matching methods to find dense correspondence and a disparity map for a rectified stereo image pair. We will also learn how to find depth maps from the disparity map. Finally, we will look at how to use depth estimation to create an obstacle avoidance system.
The rest of the content is organized as follows:
- Block matching for dense stereo correspondence.
- From disparity map to depth map.
- Obstacle avoidance system.
- Comparison with the OpenCV AI Kit with Depth (OAK-D).
- Summary.
Block Matching For Dense Stereo Correspondence
Given we have a horizontal stereo camera setup, the corresponding points for a rectified stereo image pair would have the same Y coordinate. So how do we go about finding the corresponding points?
One can think of a naive approach to compare the pixel values in the same row of the stereo image pair. However, this is not a robust method. Multiple pixels corresponding to different images can have the same pixel intensity. Moreover, considering practical constraints such as differences in the imaging sensors or exposure values, corresponding pixels may have unequal pixel values.
The working of the Block Matching Algorithm
A better approach is to consider some neighboring pixels as well. This is what we do in the block-matching algorithm. The row which we scan for stereo correspondence is called scanline. This sounds great! But how do we quantify the best match? Is there any metric that can be used to quantify how well the windows match?
There are multiple metrics, such as the Sum of Absolute Differences (SAD), Sum of Squared Differences (SSD), and Normalized Cross Correlation (NCC), that can be used to quantify the match. For example, the pair with the lowest SAD score is the best match, as the overall pixel-wise sum is the least. Figure 1 shows the scanline and reference block in the stereo image pair. The plot for SAD of the respective scanline is shown in the rightmost image.
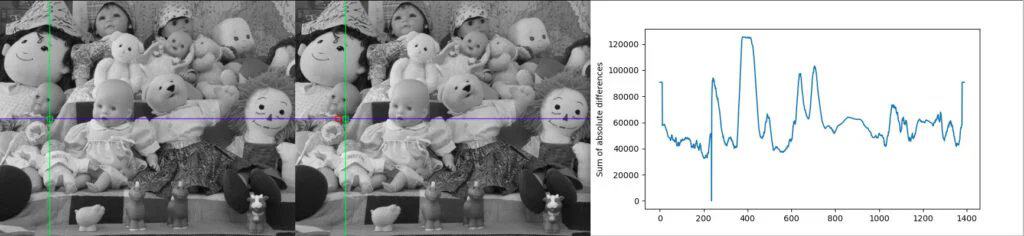
Center image shows the scanline (blue), best matching block (green) and second best matching block(red).
The right image is the plot for Sum of Absolute Difference (SAD) between the reference block from the left image, and the sliding window along the scanline in the right image.
The above method gives us only one corresponding pair. We want to find correspondence for all the pixels on the scanline. A straightforward solution is to repeat the process for all the pixels on the scanline. However, this will lead to a noisy output. Practically it is impossible to get a one-to-one correspondence for any scanline. There can be multiple matches for a given block (in case of repeating texture or texture-less regions), or there can be no ideal match (due to occlusion).
Dynamic Programming and the Scanline
Dynamic programming is a standard method to enforce a scanline’s one-to-one correspondence. The aim is to find the one-to-one correspondence for the scanline, which results in the least possible overall cost, so we overcome the practical challenges mentioned above.
Figure 2 shows SAD values for a given scanline. The left figure corresponds to a stereo image pair of unique images, and the right figure shows the SAD values for the same scanline when a single image is used, passing it twice for comparison.
SAD Values Explained
Brighter values represent a greater mismatch, and darker values represent a better match. To find the correspondence, we need to find the path from the bottom left corner to the top right corner such that the sum of values covered by the path is minimum. In the case of the right image of Figure 2, such a path is clearly visible along the diagonal (a thin black line from the bottom left corner to the top right corner). In the case of the left figure, the diagonal line contains some brighter values as well (due to occlusion, there is no matching block hence even the least SAD value is relatively bright).
OpenCV provides an implementation for the Block Matching algorithm – StereoBM class. The method of the StereoBM class calculates a disparity map for a pair of rectified stereo images. Various combinations of a stereo camera setup are possible depending on the type of camera sensors, the distance between the cameras, and many other factors. Hence, a fixed set of parameters cannot give good quality of disparity map for all possible combinations of a stereo camera setup.
GUI To Tune Parameters of Block Matching Algorithm
In this section, we create a GUI to tune the block-matching algorithm’s parameters to improve the output disparity map. We use OpenCV GUI tools to create trackbars to change the parameters. The code is shared in C++ and Python.
C++
#include <opencv2/opencv.hpp>
#include <opencv2/calib3d/calib3d.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <stdio.h>
#include <iostream>
#include "opencv2/imgcodecs.hpp"
// initialize values for StereoSGBM parameters
int numDisparities = 8;
int blockSize = 5;
int preFilterType = 1;
int preFilterSize = 1;
int preFilterCap = 31;
int minDisparity = 0;
int textureThreshold = 10;
int uniquenessRatio = 15;
int speckleRange = 0;
int speckleWindowSize = 0;
int disp12MaxDiff = -1;
int dispType = CV_16S;
// Creating an object of StereoSGBM algorithm
cv::Ptr<cv::StereoBM> stereo = cv::StereoBM::create();
cv::Mat imgL;
cv::Mat imgR;
cv::Mat imgL_gray;
cv::Mat imgR_gray;
// Defining callback functions for the trackbars to update parameter values
static void on_trackbar1( int, void* )
{
stereo->setNumDisparities(numDisparities*16);
numDisparities = numDisparities*16;
}
static void on_trackbar2( int, void* )
{
stereo->setBlockSize(blockSize*2+5);
blockSize = blockSize*2+5;
}
static void on_trackbar3( int, void* )
{
stereo->setPreFilterType(preFilterType);
}
static void on_trackbar4( int, void* )
{
stereo->setPreFilterSize(preFilterSize*2+5);
preFilterSize = preFilterSize*2+5;
}
static void on_trackbar5( int, void* )
{
stereo->setPreFilterCap(preFilterCap);
}
static void on_trackbar6( int, void* )
{
stereo->setTextureThreshold(textureThreshold);
}
static void on_trackbar7( int, void* )
{
stereo->setUniquenessRatio(uniquenessRatio);
}
static void on_trackbar8( int, void* )
{
stereo->setSpeckleRange(speckleRange);
}
static void on_trackbar9( int, void* )
{
stereo->setSpeckleWindowSize(speckleWindowSize*2);
speckleWindowSize = speckleWindowSize*2;
}
static void on_trackbar10( int, void* )
{
stereo->setDisp12MaxDiff(disp12MaxDiff);
}
static void on_trackbar11( int, void* )
{
stereo->setMinDisparity(minDisparity);
}
int main()
{
// Initialize variables to store the maps for stereo rectification
cv::Mat Left_Stereo_Map1, Left_Stereo_Map2;
cv::Mat Right_Stereo_Map1, Right_Stereo_Map2;
// Reading the mapping values for stereo image rectification
cv::FileStorage cv_file2 = cv::FileStorage("data/stereo_rectify_maps.xml", cv::FileStorage::READ);
cv_file2["Left_Stereo_Map_x"] >> Left_Stereo_Map1;
cv_file2["Left_Stereo_Map_y"] >> Left_Stereo_Map2;
cv_file2["Right_Stereo_Map_x"] >> Right_Stereo_Map1;
cv_file2["Right_Stereo_Map_y"] >> Right_Stereo_Map2;
cv_file2.release();
// Check for left and right camera IDs
// These values can change depending on the system
int CamL_id{2}; // Camera ID for left camera
int CamR_id{0}; // Camera ID for right camera
cv::VideoCapture camL(CamL_id), camR(CamR_id);
// Check if left camera is attached
if (!camL.isOpened())
{
std::cout << "Could not open camera with index : " << CamL_id << std::endl;
return -1;
}
// Check if right camera is attached
if (!camL.isOpened())
{
std::cout << "Could not open camera with index : " << CamL_id << std::endl;
return -1;
}
// Creating a named window to be linked to the trackbars
cv::namedWindow("disparity",cv::WINDOW_NORMAL);
cv::resizeWindow("disparity",600,600);
// Creating trackbars to dynamically update the StereoBM parameters
cv::createTrackbar("numDisparities", "disparity", &numDisparities, 18, on_trackbar1);
cv::createTrackbar("blockSize", "disparity", &blockSize, 50, on_trackbar2);
cv::createTrackbar("preFilterType", "disparity", &preFilterType, 1, on_trackbar3);
cv::createTrackbar("preFilterSize", "disparity", &preFilterSize, 25, on_trackbar4);
cv::createTrackbar("preFilterCap", "disparity", &preFilterCap, 62, on_trackbar5);
cv::createTrackbar("textureThreshold", "disparity", &textureThreshold, 100, on_trackbar6);
cv::createTrackbar("uniquenessRatio", "disparity", &uniquenessRatio, 100, on_trackbar7);
cv::createTrackbar("speckleRange", "disparity", &speckleRange, 100, on_trackbar8);
cv::createTrackbar("speckleWindowSize", "disparity", &speckleWindowSize, 25, on_trackbar9);
cv::createTrackbar("disp12MaxDiff", "disparity", &disp12MaxDiff, 25, on_trackbar10);
cv::createTrackbar("minDisparity", "disparity", &minDisparity, 25, on_trackbar11);
cv::Mat disp, disparity;
while (true)
{
// Capturing and storing left and right camera images
camL >> imgL;
camR >> imgR;
// Converting images to grayscale
cv::cvtColor(imgL, imgL_gray, cv::COLOR_BGR2GRAY);
cv::cvtColor(imgR, imgR_gray, cv::COLOR_BGR2GRAY);
// Initialize matrix for rectified stereo images
cv::Mat Left_nice, Right_nice;
// Applying stereo image rectification on the left image
cv::remap(imgL_gray,
Left_nice,
Left_Stereo_Map1,
Left_Stereo_Map2,
cv::INTER_LANCZOS4,
cv::BORDER_CONSTANT,
0);
// Applying stereo image rectification on the right image
cv::remap(imgR_gray,
Right_nice,
Right_Stereo_Map1,
Right_Stereo_Map2,
cv::INTER_LANCZOS4,
cv::BORDER_CONSTANT,
0);
// Calculating disparith using the StereoBM algorithm
stereo->compute(Left_nice,Right_nice,disp);
// NOTE: Code returns a 16bit signed single channel image,
// CV_16S containing a disparity map scaled by 16. Hence it
// is essential to convert it to CV_32F and scale it down 16 times.
// Converting disparity values to CV_32F from CV_16S
disp.convertTo(disparity,CV_32F, 1.0);
// Scaling down the disparity values and normalizing them
disparity = (disparity/16.0f - (float)minDisparity)/((float)numDisparities);
// Displaying the disparity map
cv::imshow("disparity",disparity);
// Close window using esc key
if (cv::waitKey(1) == 27) break;
}
return 0;
}
Python
import numpy as np
import cv2
# Check for left and right camera IDs
# These values can change depending on the system
CamL_id = 2 # Camera ID for left camera
CamR_id = 0 # Camera ID for right camera
CamL= cv2.VideoCapture(CamL_id)
CamR= cv2.VideoCapture(CamR_id)
# Reading the mapping values for stereo image rectification
cv_file = cv2.FileStorage("data/stereo_rectify_maps.xml", cv2.FILE_STORAGE_READ)
Left_Stereo_Map_x = cv_file.getNode("Left_Stereo_Map_x").mat()
Left_Stereo_Map_y = cv_file.getNode("Left_Stereo_Map_y").mat()
Right_Stereo_Map_x = cv_file.getNode("Right_Stereo_Map_x").mat()
Right_Stereo_Map_y = cv_file.getNode("Right_Stereo_Map_y").mat()
cv_file.release()
def nothing(x):
pass
cv2.namedWindow('disp',cv2.WINDOW_NORMAL)
cv2.resizeWindow('disp',600,600)
cv2.createTrackbar('numDisparities','disp',1,17,nothing)
cv2.createTrackbar('blockSize','disp',5,50,nothing)
cv2.createTrackbar('preFilterType','disp',1,1,nothing)
cv2.createTrackbar('preFilterSize','disp',2,25,nothing)
cv2.createTrackbar('preFilterCap','disp',5,62,nothing)
cv2.createTrackbar('textureThreshold','disp',10,100,nothing)
cv2.createTrackbar('uniquenessRatio','disp',15,100,nothing)
cv2.createTrackbar('speckleRange','disp',0,100,nothing)
cv2.createTrackbar('speckleWindowSize','disp',3,25,nothing)
cv2.createTrackbar('disp12MaxDiff','disp',5,25,nothing)
cv2.createTrackbar('minDisparity','disp',5,25,nothing)
# Creating an object of StereoBM algorithm
stereo = cv2.StereoBM_create()
while True:
# Capturing and storing left and right camera images
retL, imgL= CamL.read()
retR, imgR= CamR.read()
# Proceed only if the frames have been captured
if retL and retR:
imgR_gray = cv2.cvtColor(imgR,cv2.COLOR_BGR2GRAY)
imgL_gray = cv2.cvtColor(imgL,cv2.COLOR_BGR2GRAY)
# Applying stereo image rectification on the left image
Left_nice= cv2.remap(imgL_gray,
Left_Stereo_Map_x,
Left_Stereo_Map_y,
cv2.INTER_LANCZOS4,
cv2.BORDER_CONSTANT,
0)
# Applying stereo image rectification on the right image
Right_nice= cv2.remap(imgR_gray,
Right_Stereo_Map_x,
Right_Stereo_Map_y,
cv2.INTER_LANCZOS4,
cv2.BORDER_CONSTANT,
0)
# Updating the parameters based on the trackbar positions
numDisparities = cv2.getTrackbarPos('numDisparities','disp')*16
blockSize = cv2.getTrackbarPos('blockSize','disp')*2 + 5
preFilterType = cv2.getTrackbarPos('preFilterType','disp')
preFilterSize = cv2.getTrackbarPos('preFilterSize','disp')*2 + 5
preFilterCap = cv2.getTrackbarPos('preFilterCap','disp')
textureThreshold = cv2.getTrackbarPos('textureThreshold','disp')
uniquenessRatio = cv2.getTrackbarPos('uniquenessRatio','disp')
speckleRange = cv2.getTrackbarPos('speckleRange','disp')
speckleWindowSize = cv2.getTrackbarPos('speckleWindowSize','disp')*2
disp12MaxDiff = cv2.getTrackbarPos('disp12MaxDiff','disp')
minDisparity = cv2.getTrackbarPos('minDisparity','disp')
# Setting the updated parameters before computing disparity map
stereo.setNumDisparities(numDisparities)
stereo.setBlockSize(blockSize)
stereo.setPreFilterType(preFilterType)
stereo.setPreFilterSize(preFilterSize)
stereo.setPreFilterCap(preFilterCap)
stereo.setTextureThreshold(textureThreshold)
stereo.setUniquenessRatio(uniquenessRatio)
stereo.setSpeckleRange(speckleRange)
stereo.setSpeckleWindowSize(speckleWindowSize)
stereo.setDisp12MaxDiff(disp12MaxDiff)
stereo.setMinDisparity(minDisparity)
# Calculating disparity using the StereoBM algorithm
disparity = stereo.compute(Left_nice,Right_nice)
# NOTE: Code returns a 16bit signed single channel image,
# CV_16S containing a disparity map scaled by 16. Hence it
# is essential to convert it to CV_32F and scale it down 16 times.
# Converting to float32
disparity = disparity.astype(np.float32)
# Scaling down the disparity values and normalizing them
disparity = (disparity/16.0 - minDisparity)/numDisparities
# Displaying the disparity map
cv2.imshow("disp",disparity)
# Close window using esc key
if cv2.waitKey(1) == 27:
break
else:
CamL= cv2.VideoCapture(CamL_id)
CamR= cv2.VideoCapture(CamR_id)
The GUI created using the above code will help us change the Block Matching algorithm’s different parameters. We can also store the parameters using the FileStorage class of OpenCV. To know more about the usage of FileStorage class, refer to our earlier post.
Understanding The Effect of Each Parameter
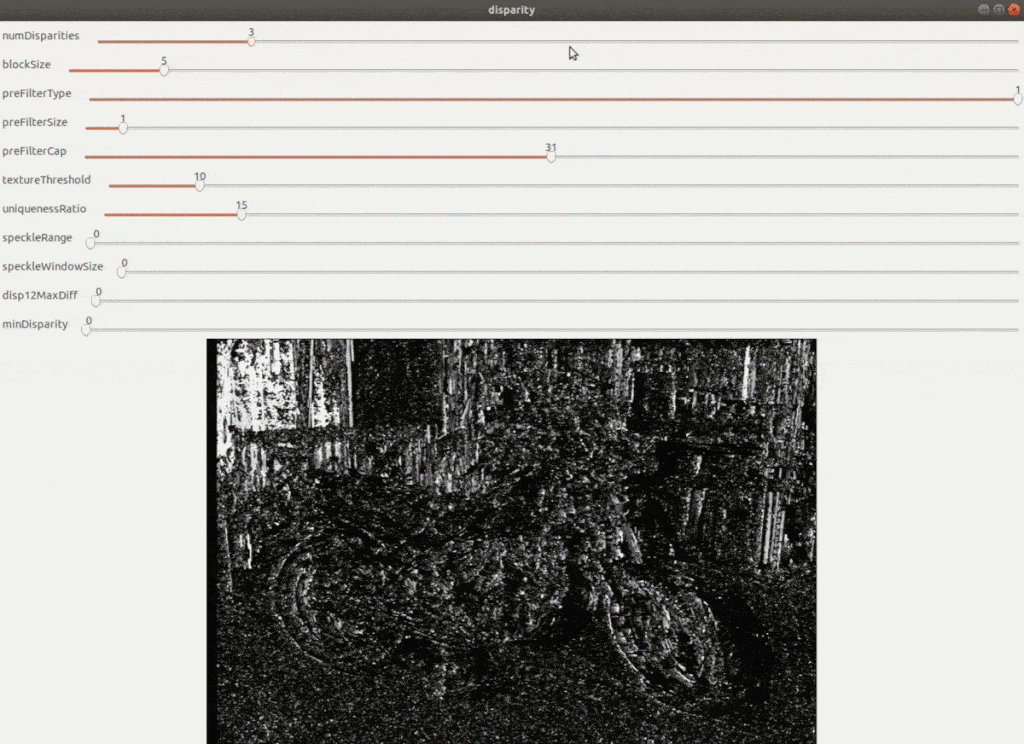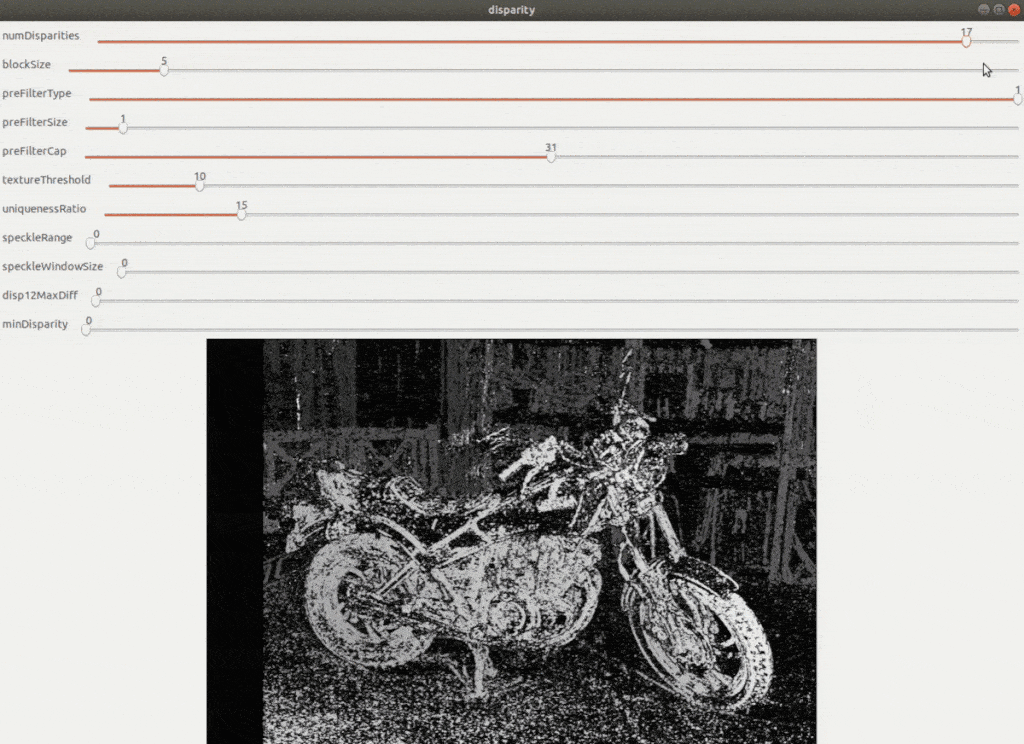
- A number of disparities (numDisparities): Sets the range of disparity values to be searched. The overall range is from minimum to minimum disparity value + several disparities. The following images show the disparity map calculated for two different disparity ranges. It is clearly visible that increasing the number of disparities increases the accuracy of the disparity map.
- Block size (blockSize): Size of the sliding window used for block matching to find corresponding pixels in a rectified stereo image pair. A higher value indicates a larger window size. The following GIF indicates that increasing this parameter results in more smooth disparity maps.

Other Parameters
- Pre-Filter Type (preFilterType): Parameter to decide the type of pre-filtering to be applied to the images before passing to the block matching algorithm. This step enhances the texture information and improves the results of the block-matching algorithm. The filter type can be CV_STEREO_BM_XSOBEL or CV_STEREO_BM_NORMALIZED_RESPONSE.
- Pre-filter size (preFilterSize): Window size of the filter used in the pre-filtering stage.
- Pre-filter cap (preFilterCap): Limits the filtered output to a specific value.
- Minimum disparity (minDisparity): The minimum value of the disparity to be searched. In most scenarios it is set to zero. It can also be set to negative value depending on the stereo camera setup.
- Texture threshold (textureThreshold): Filters out areas that do not have enough texture information for reliable matching.
- Uniqueness Ratio (uniquenessRatio): Another post-filtering step. The pixel is filtered out if the best matching disparity is not sufficiently better than every other disparity in the search range. The following GIF depicts that increasing the uniqueness ratio increases the number of pixels that are filtered out.

Other Parameters, continued.
- Speckle range (speckleRange) and speckle window size (speckleWindowSize): Speckles are produced near the boundaries of the objects, where the matching window catches the foreground on one side and the background on the other. To get rid of these artifacts, we apply speckle filter which has two parameters. The speckle range defines how close the disparity values should be to be considered as part of the same blob. The speckle window size is the number of pixels below which a disparity blob is dismissed as “speckle”.
- disp12MaxDiff: Pixels are matched both ways, from the left image to the right image and from the right image to left image. disp12MaxDiff defines the maximum allowable difference between the original left pixel and the back-matched pixel.
A significant point to note is that the method of the block matching class returns a 16-bit signed single-channel image containing disparity values scaled by 16. Hence, to get the actual disparity values from such fixed-point representation, we need to divide the disparity values by 16.
OpenCV also provides StereoSGBM, which implements Hirschmüller’s original SGM [2] algorithm. SGBM stands for Semi-Global Block Matching. It also implements the sub-pixel estimation proposed by Brichfield et al. [3]
In the case of simple block matching, sometimes using the minimum cost can give wrong matches. Note that wrong matches can have a lower cost than correct matches. Hence SGBM applies additional constraints to increase smoothness by penalizing changes of disparities in the 8-connected neighborhood. For the constraint, 1-D minimum cost paths from multiple directions are aggregated.
The block-matching-based algorithms are classical computer vision algorithms. After the advent of deep neural networks, several deep learning architectures have been proposed to find dense correspondence between a stereo image pair. For further details, refer to our article on stereo matching.
From disparity map to depth map
Till now, the grayscale images we have been obtaining are just the disparity maps and not the depth maps. Using block matching methods, we calculated dense correspondences for a rectified stereo image pair.. We calculated the disparity for each pixel with the help of these dense correspondences ( shift between the corresponding pixels). Our earlier article on epipolar geometry provides a good intuition of how disparity is related to depth.
In this post, we improve our understanding of how depth relates to disparity and derive an expression for calculating depth from disparity. The following figure helps visualize the derivation of the expression.
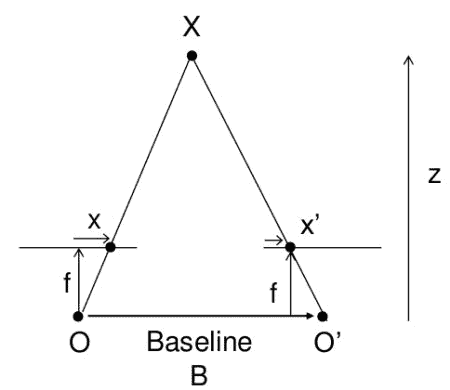
From the above figure, we can derive the relation between disparity (x – x’) and depth Z as follows:
(1) ![]()
Here B is the baseline of the stereo camera setup, and f is the focal length.
Now in the case of a practical setup, the focal length f of both the cameras is not identical, and moreover, manually measuring B can also lead to errors. This leads us to an important question – what should be the value of f and B, and how do we derive it?
We derive it experimentally. The above equation can also be written as follows:
(2) ![]()
Where
(3) ![]()
By creating a GUI that displays a targeted pixel’s disparity values, we can practically measure its distance from the camera (Z). Based on multiple disparity readings and Z (depth), we can solve for M by formulating a least-squares problem. The following graphs depict the relation between depth and disparity for a stereo camera setup highlighting the data points obtained from different observations.
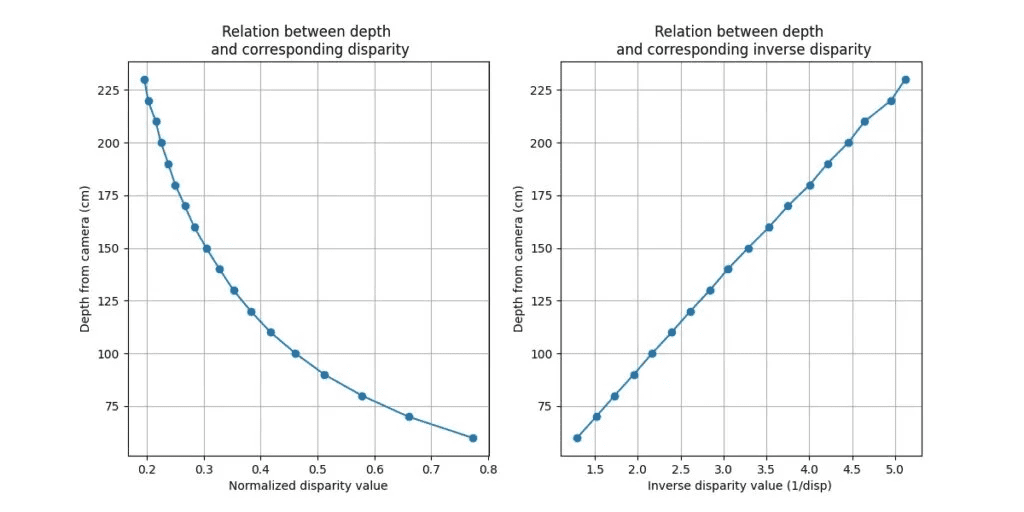
Okay! The least-squares problem sounds fun. But what exactly does it mean? And how do we code it?
First, we will rearrange the previous equation as follows:
(4) ![]()
By substituting
(5) ![]()
we get the following equation:
(6) ![]()
This is relatively easy, right? We need a single reading of (Z,a) to calculate M (One equation, one variable). Why do we need multiple readings, and why do we use the least-squares method? Well, this is because nothing is perfect in a practical world!
There is always a chance of error when we talk about practical scenarios. In this case, there can be a human error (in measuring the distance Z), or the disparity values calculated by the algorithm can be a bit inaccurate. Also, quantization of the disparity values induces some error. Hence, depending on a single reading is not a good idea.
So, we take multiple readings of (Z,a). Hence the number of equations exceeds the number of variables. The least-squares method helps find the value of M that best agrees with all the readings. Graphically, it is the process of finding a line such that the sum of squared distances of all the data points from the line is the least.
We can use the solve() method of OpenCV to find the solution to the least-squares approximation problem. A sample code is shared below:
Python
# solving for M in the following equation
# || depth = M * (1/disparity) ||
# for N data points coeff is Nx2 matrix with values
# 1/disparity, 1
# and depth is Nx1 matrix with depth values
ret, sol = cv2.solve(coeff,z,flags=cv2.DECOMP_QR)
C++
//solving for M in the following equation
//|| depth = M * (1/disparity) ||
//for N data points coeff is Nx2 matrix with values
//1/disparity, 1
//and depth is Nx1 matrix with depth values
cv::Mat Z_mat(z_vec.size(), 1, CV_32F, z_vec.data());
cv::Mat coeff(z_vec.size(), 2, CV_32F, coeff_vec.data());
cv::Mat sol(2, 1, CV_32F);
float M;
// Solving for M using least square fitting with QR decomposition method
cv::solve(coeff, Z_mat, sol, cv::DECOMP_QR);
M = sol.at<float>(0,0);
Once we solve for M, we can convert the disparity map to the depth map by adding the following equation to our code after calculating the disparity map:
(7) ![]()
The following video illustrates the process of capturing multiple readings of disparity values and corresponding depth values using the code shared with this post. It is better to take as many readings as possible for a more accurate solution.
Awesome! We now know how a disparity map is calculated using a block-matching algorithm and how to tune the parameters to give us a good disparity map for a stereo camera setup. We also know how to get the depth map from a disparity map.
Hence, we can make a computer perceive depth! Let us use this to create an engaging application! We will create an obstacle avoidance system with a stereo camera setup. It will be similar to the one demonstrated in the video shared at the beginning of this post.
Obstacle avoidance system
The basic concept of obstacle avoidance is determining if the distance of any object from the sensor is closer than the minimum threshold distance. In our case, the sensor is a stereo camera. Another type of device widely used for distance measurement and obstacle avoidance is an ultrasonic sensor.
Unlike stereo cameras, ultrasonic sensors work on the propagation of signals. A signal of known frequency is emitted. It travels until an object obstructs its path. It gets reflected from the object, and the sensor receives the reflected signal. If the signal’s speed is known, the time elapsed between the transmission and receiving of the signal can be used to calculate the object’s distance from the sensor. Bats use a similar method to navigate and avoid obstacles.
A stereo camera’s key advantage over an ultrasonic sensor is that the stereo camera provides a greater field of view.
Steps to build an obstacle avoidance system
So how do we create an obstacle avoidance system using a stereo camera? The steps to build such a system are as follows:
- Get the depth map from the stereo camera.
- Based on a threshold (minimum depth value), determine regions in the depth map with a depth value less than the threshold. Using the inRange() method, create a mask to segment such regions.
- Apply contour detection and find the largest contour.
- Create a new mask using the largest contour.
- Find the average depth value using the meanStdDev() method using the mask created in step 4.
- Perform the warning action. In our example, we display the distance of the obstacle in red color.
Following is the code for the obstacle avoidance system.
Python
depth_thresh = 100.0 # Threshold for SAFE distance (in cm)
# Mask to segment regions with depth less than threshold
mask = cv2.inRange(depth_map,10,depth_thresh)
# Check if a significantly large obstacle is present and filter out smaller noisy regions
if np.sum(mask)/255.0 > 0.01*mask.shape[0]*mask.shape[1]:
# Contour detection
contours, _ = cv2.findContours(mask, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
cnts = sorted(contours, key=cv2.contourArea, reverse=True)
# Check if detected contour is significantly large (to avoid multiple tiny regions)
if cv2.contourArea(cnts[0]) > 0.01*mask.shape[0]*mask.shape[1]:
x,y,w,h = cv2.boundingRect(cnts[0])
# finding average depth of region represented by the largest contour
mask2 = np.zeros_like(mask)
cv2.drawContours(mask2, cnts, 0, (255), -1)
# Calculating the average depth of the object closer than the safe distance
depth_mean, _ = cv2.meanStdDev(depth_map, mask=mask2)
# Display warning text
cv2.putText(output_canvas, "WARNING !", (x+5,y-40), 1, 2, (0,0,255), 2, 2)
cv2.putText(output_canvas, "Object at", (x+5,y), 1, 2, (100,10,25), 2, 2)
cv2.putText(output_canvas, "%.2f cm"%depth_mean, (x+5,y+40), 1, 2, (100,10,25), 2, 2)
else:
cv2.putText(output_canvas, "SAFE!", (100,100),1,3,(0,255,0),2,3)
cv2.imshow('output_canvas',output_canvas)
C++
float depth_thresh = 100.0; // Threshold for SAFE distance (in cm)
cv::Mat mask, mean, stddev, mask2;
// Mask to segment regions with depth less than safe distance
cv::inRange(depth_map, 10, depth_thresh, mask);
double s = (cv::sum(mask)[0])/255.0;
double img_area = double(mask.rows * mask.cols);
std::vector<std::vector<cv::Point>> contours;
std::vector<cv::Vec4i> hierarchy;
// Check if a significantly large obstacle is present and filter out smaller noisy regions
if (s > 0.01*img_area)
{
// finding conoturs in the generated mask
cv::findContours(mask, contours, hierarchy, cv::RETR_TREE, cv::CHAIN_APPROX_SIMPLE);
// sorting contours from largest to smallest
std::sort(contours.begin(), contours.end(), compareContourAreas);
// extracting the largest contour
std::vector<cv::Point> cnt = contours[0];
// Check if detected contour is significantly large (to avoid multiple tiny regions)
double cnt_area = fabs( cv::contourArea(cv::Mat(cnt)));
if (cnt_area > 0.01*img_area)
{
cv::Rect box;
// Finding the bounding rectangle for the largest contour
box = cv::boundingRect(cnt);
// finding average depth of region represented by the largest contour
mask2 = mask*0;
cv::drawContours(mask2, contours, 0, (255), -1);
// Calculating the average depth of the object closer than the safe distance
cv::meanStdDev(depth_map, mean, stddev, mask2);
// Printing the warning text with object distance
char text[10];
std::sprintf(text, "%.2f cm",mean.at<double>(0,0));
cv::putText(output_canvas, "WARNING!", cv::Point2f(box.x + 5, box.y-40), 1, 2, cv::Scalar(0,0,255), 2, 2);
cv::putText(output_canvas, "Object at", cv::Point2f(box.x + 5, box.y), 1, 2, cv::Scalar(0,0,255), 2, 2);
cv::putText(output_canvas, text, cv::Point2f(box.x + 5, box.y+40), 1, 2, cv::Scalar(0,0,255), 2, 2);
}
}
else
{
// Printing SAFE if no obstacle is closer than the safe distance
cv::putText(output_canvas, "SAFE!", cv::Point2f(200,200),1,2,cv::Scalar(0,255,0),2,2);
}
// Displaying the output of the obstacle avoidance system
cv::imshow("output_canvas",output_canvas);
Following video shows the output of the obstacle avoidance system discussed in this post:
Comparison With OpenCV AI Kit with Depth (OAK-D).
In our earlier posts, we created a custom low-cost stereo camera setup and calibrated it to capture anaglyph 3D videos. In this post, we used the calibrated stereo camera setup for depth estimation.
Based on this experience, it is clear that building a custom stereo camera is a time-consuming and involved process. From stereo rectification and camera calibration to fine-tuning the block-matching parameters and finding the mapping between depth maps and disparity values, it covers major fundamental concepts of stereo vision. Hence, it is an excellent exercise for any computer vision enthusiast interested in stereo vision and classical computer vision.
However, one might be more interested in using depth maps for downstream tasks such as 3D reconstruction or autonomous navigation. In such a case, building a custom stereo camera might not be the best option. Moreover, we also observed that block matching is a computationally intense process. Hence, running it on any edge device like Raspberry Pi might consume a significant fraction of computation power.
Hence, OpenCV AI Kit with Depth (OAK-D) is a blessing to all computer vision enthusiasts. OAK-D has a stereo camera along with an RGB camera. Additionally, it has its own processing unit (Intel Myriad X for Deep Learning Inference). The best part is that we no longer have to run the depth estimation algorithm on the host system. OAK-D returns frames captured by the RGB camera, the stereo camera, and also the corresponding depth map. With just a few code lines, you get a depth map without using any computational power of the host system.
See OAK-D in Action
I know you are already amazed by the power of OAK-D, but depth maps are just the tip of the iceberg. We realize OAK-D’s true potential when we also want to run a deep learning model for tasks such as object detection. Yes! You guessed it right! OAK-D can also run deep-learning model predictions.
As mentioned earlier, OAK-D comes with loads of advantages: a stereo camera and an RGB camera, its own processing unit (Intel Myriad X for Deep Learning Inference), and the ability to run a deep learning model for tasks such as object detection. Watch the following video to see the OAK-D in action and to know about its amazing capabilities.
Interested in OAK-D? Want to buy it? Please visit the store by clicking here.
Summary
This article is the third of our series on Introduction to Spatial AI. This post discussed classical methods for stereo matching and depth estimation using Stereo Camera and OpenCV.
We started with the problem statement: using stereo vision-based depth estimation for robots autonomously navigating or grasping different objects or avoiding collisions while moving around. We also gave a recap of the learnings from the first two posts of this series.
We discussed in detail the theory behind Block Matching for Dense Stereo Correspondence. We learned that a fixed set of parameters would not give a good quality disparity map for all possible combinations of a stereo camera setup. To overcome this shortfall, we created a GUI that helps us change different parameters of the Block Matching algorithm. Another important takeaway is that when using the minimum cost, simple block matching can give the wrong match. The reason is wrong matches can have a lower cost than correct matches.
Next, we discussed how depth is related to the disparity. We derived an expression for calculating depth from disparity, making a computer perceive depth.
Then, we discussed the basic concept of obstacle avoidance: to determine if the distance of any object from the sensor is closer than the minimum threshold distance. We built a code for a practical, problem-solving obstacle avoidance system.
Finally, we compared a custom low-cost stereo camera setup and calibrated it to capture anaglyph 3D with OpenCV AI Kit with Depth (OAK-D).
A friendly reminder that you would need prior knowledge to understand the concepts and content of this article. We would encourage you to review the articles suggested at the start of this post. Please let us know your experience and learning outcomes from this post using the comments section.
Subscribe & Download Code
If you liked this article and would like to download code (C++ and Python) and example images used in this post, please click here. Alternately, sign up to receive a free Computer Vision Resource Guide. In our newsletter, we share OpenCV tutorials and examples written in C++/Python, and Computer Vision and Machine Learning algorithms and news.References
[1] C. Loop and Z. Zhang. Computing Rectifying Homographies for Stereo Vision. IEEE Conf. Computer Vision and Pattern Recognition, 1999.
[2] Hirschmüller, Heiko (2005). “Accurate and efficient stereo processing by semi-global matching and mutual information”. IEEE Conference on Computer Vision and Pattern Recognition. pp. 807–814.
[3] . Birchfield and C. Tomasi, “Depth discontinuities by pixel-to-pixelstereo,”International Journal of Computer Vision, vol. 35, no. 3,pp. 269–293, 1999.
[4] Similar stereo camera project. GitHub link – https://github.com/LearnTechWithUs/Stereo-Vision