YOLO Loss Function Part 2: GFL and VFL Loss

yolo v1 loss function
yolo v8 loss function
keras yolo custom loss function
keras yolo loss function
Yolo loss function example
yolo v8 loss function
yolo loss function python
yolo loss function pytorch
yolo loss function implementation
yolov3 loss function
Yolo loss function in object detection
yolo loss function explained
yolo loss function

In the preceding article, YOLO Loss Functions Part 1, we focused exclusively on SIoU and Focal Loss as the primary loss functions used in the YOLO series of models. In this article, we will dive deeper into the YOLO loss function and explore two other interesting loss functions: Generalized Focal Loss (GFL) and Varifocal Loss(VFL). Both of the loss functions are widely utilized in object detection tasks. GFL has two parts:

Quality Focal Loss (QFL) for classification and localization quality estimation
Distribution Focal Loss (DFL) for bounding box regression.

In YOLOv8, DFL was utilized for bounding box regression, while YOLOv6 applied VFL for the classification task. Gaining insight into these loss functions allows us to comprehend the design decisions and the typical challenges object detection encounters in striving for both efficiency and precision in its results.

The structure of the article is outlined as follows: We will explore Generalized Focal Loss (GFL) and Varifocal Loss (VFL), focusing on the challenges they aim to solve, the solutions they introduce, and end with a PyTorch code implementation for both loss functions.

Generalized Focal Loss (GFL):
Varifocal Loss:
Key Takeaways
Conclusion
References

Generalized Focal Loss (GFL):

Generalized Focal Loss(GFL) was published in NeurIPs 2020 by Li et al. A quick glance over the paper will give you a sense that it is rich in information and worth reading. In the era of white paper reports, computational, and data-driven research, this paper presents a clear problem statement and seeks to address it through a sophisticated, mathematically derived method. By doing so, this paper sits along the lines of YOLOv4, YOLOv7, FCOS, etc. One of the key aspects of this paper is that it brings up a probabilistic point of view on object detection, which is very important in a highly complex, unstructured world. It may be a bit overwhelming for a beginner to go through the entire paper and understand the introduced concepts thoroughly, as it is a math-heavy paper. But we will try to make this article a medium to explain the concepts as easily as possible.

yolo v8 loss function: yolo v6 loss function

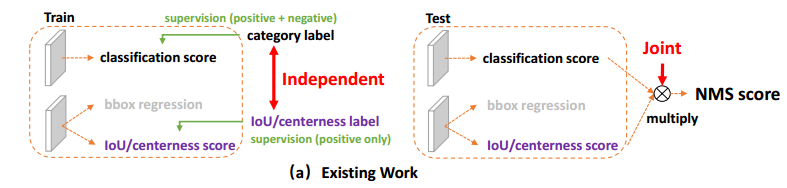
Figure 1: Comparisons between existing separate representation and proposed joint representation of classification and localization quality estimation.

Before proceeding forward, it’s important to understand the problems that this loss function is solving.

Combining Localization Quality Estimate and Classification Score

In earlier days, researchers understood that when the research was moving toward single-stage dense bounding box prediction, people were not giving much attention to bounding box representation and localization. Then, the FCOS paper emerged, where the authors introduced a separate branch for IoU or centerness score prediction, also known as the Localization Quality Estimation branch. Then, the Localization score is combined(multiplied) with the classification confidence for ranking bounding boxes in NMS(Non-Max-Suppression). The localization quality prediction is done by taking only the positive samples.

Despite the success, there was always a chance of false positives being ranked higher in the NMS but, at the same time, missing out on true positives. Like below example given in the paper,

yolo v8 loss function
yolo loss function python

Figure 2: Unreliable IoU predictions of current dense detector with IoU-branch.

In image A, the classification score is given as 0.095, which suggests that it’s unlikely to be an object of interest. However, with a predicted IoU score of 0.927, there is considerable overlap between the predicted and actual ground truth bounding boxes. Image A is considered a false positive due to its high IoU but low Classification Score. Similarly, image B’s classification score is low(0.101), indicating it is likely background, and, at the same time, it has an IoU of 0.913, meaning that the instance is a false positive.

Now, multiplying the IoU and the Classification score might lead to a high value, making it suitable for NMS ranking. Still, the fact that it has a low classification score makes it a negative example.

These issues caused problems with accurately combining the IoU score with the Classification Score for better NMS ranking of dense prediction.

Inflexible representation of bounding boxes

Another problem that generally appears is, the distribution of target bounding box coordinates is represented as a Dirac delta distribution. Former loss functions typically employ the Dirac Delta distribution to denote the target coordinate distribution. This means that these loss functions were used to pinpoint the bounding box coordinates to match the bounding box location from the ground truth exactly. However, it fails to consider the ambiguity and uncertainty in datasets. Although some recent works tried modeling the bounding boxes as a Gaussian distribution, constraining a real distribution as a fixed distribution is impossible as it is supposed to be more arbitrary and flexible.

What is Dirac delta distribution?

Dirac delta distribution (or δ distribution) is known as unit impulse. The value of this function is zero everywhere except at zero. At zero, the value of the Dirac delta function is 1. So, intuitively, the integral of this function over the entire real line(from positive infinity to negative infinity) is equal to one. This function is represented below.

yolo loss function implementation
yolov3 loss function

Figure 3: a) Dirac Delta Function, b) Dirac Delta Distribution plot

The real world is uncertain, and modeling a problem to precisely predict the bounding box location is not feasible. Having a probabilistic approach to solve this problem is very important, as the objective should be predicting the bounding box coordinates at the same area as the ground truth bounding box.

Solutions Introduced:

As the solution to the problems mentioned above, the authors came up with the idea of predicting a single value for representing the localization quality and the classification score; they called this “classification-IoU joint representation”. The loss function is designed to be trained in an end-to-end fashion while being utilized during inference. As a result, it helps with train-test inconsistency and enables a strong correlation between the localization quality and classification score, as shown in Figure 4,

keras yolo custom loss function
keras yolo loss function
Yolo loss function example
yolo v8 loss function
yolo loss function python
pytorch yolo custom loss function

Figure 4: The scatter diagram of localization and classification score

The above is a plot between the localization score and the classification score. The blue points represent the weak correlation between the two scores; this happens because of separate representations. The red points represent the false positives, where the classification score is low, but the IoU score is high. The green points are the examples trained using the GFL loss function; here, both scores are strongly correlated because the joint representation forces them to be equal. Generally, the classification problem is solved using the Focal loss, which takes care of the dataset imbalance problem. However, when introducing this loss function for joint representation of localization quality and classification score, they faced the problem of continuous IoU labels (0 to 1) coming out of the model. On the other hand, Focal Loss only supports discrete {0,1} category labels. To understand this statement more clearly, let’s first go through the below statement,

yolo loss function python
yolo loss function pytorch
yolo loss function implementation
yolov3 loss function

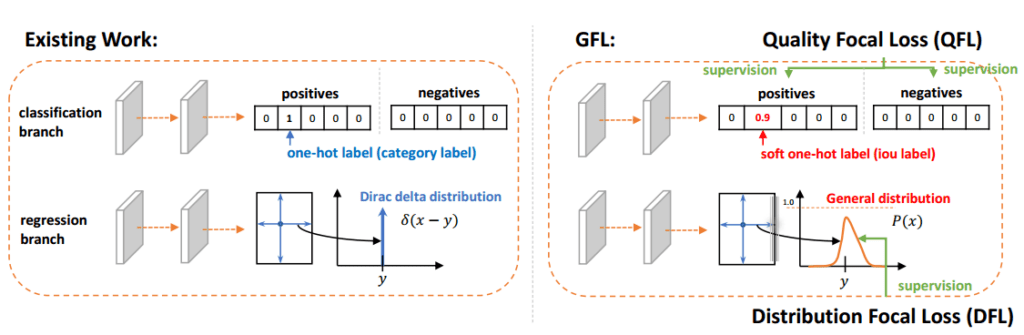
Figure 5: The comparisons between conventional methods and our proposed GFL in the head of dense detectors. GFL includes QFL and DFL.

We present a joint representation of localization quality (i.e., IoU score) and classification score (“classification-IoU” for short), where its supervision softens the standard one-hot category label and leads to a possible float target y belongs to [0; 1] on the corresponding category.

A classification vector where its value at the ground-truth category index refers to its corresponding localization quality.

This means the model predicts the classes as a one-hot encoding. But, instead of having 0s and 1s, they have continuous values in the class index. See Figure 4, in the GFL classification branch positives part, you can see that the one-hot encoded vector has a continuous value. The index of this continuous value indicates the predicted class id, and the continuous value is the predicted IoU for quantifying the localization quality. They made the representation in such a way that the “classification-IoU score” is proportional to the classification score as well as the IoU score.

To solve the 2nd problem, they decided to learn the discretized probability distribution of the bound box coordinates over its continuous space without introducing any strong priors.

But, this question might come your mind that, If the IoU-Classification branch is not connected with the bbox regression branch, then how its predicting the IoU? Furthermore, what target value used for the Localization Quality prediction?

This approach holds by four key reasons:
1. IoU prediction acts as a proxy(replacement/stand-in) for the localization quality prediction.
2. The point is, the objective of clf-iou branch is not to find out the actual IoU value between the prediction and ground truth, its there to predict the most likely IoU value between them, based on the visual features and the context of the object within the image. (Answers the 2nd question)
3. As the clf-iou branch trying to predict the IoU score, it needs a target value for calculating the loss. Here, the target is the actual IoU calculated through predicted and the Ground truth coordinates.
4. The whole training is end-to-end, means the clf-iou branch, bounding box regression branch all are trained as a unified entity, which means that there are join representation between both the branches.

We have already discussed Focal Loss in our previous article, but let’s quickly go through the idea behind Focal Loss.

Focal Loss Recap:

Focal loss is a dynamically scaled binary cross-entropy loss. It is reliable for class imbalance problems, where an extreme imbalance between foreground and background classes often exists during training. This is a modified version of the binary cross-entropy loss function,

Figure 6: Focal Loss Equation

Here, $\alpha$ is the weighting factor, $\gamma$ is the modulating factor, and $p_t$ is the probability of the true class. The use of the modulating factor is to dump down the contribution of the majority classes(easy examples), and the use of $\alpha$ was to assign weights to the data point to counter the class imbalance problem.

Quality Focal Loss

QFL solves the first problem by creating a joint representation of Localization Quality and Classification Score. It also solves the continuous IoU labels issue. The suggested classification-IoU combined representation necessitates comprehensive supervision throughout the whole image, and since issues with class imbalance persist, it is essential to retain the principles of Focal Loss.

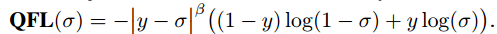
Figure 7: Quality Focal Loss Equation

The second part of the QFL loss is copied from the binary cross entropy loss. Here,

σ: The prediction made by the model after being processed by a sigmoid function makes it a value between 0 and 1.

y: The true value or label, which in the context of this discussion is between 0 and 1.

β: This parameter controls the down-weighting rate (experimentally, the authors found that β=2 works better).

In the first part, where the scaling factor is applied, we replace that with the absolute distance between the estimation $\sigma$ and its continuous label y. y=0 denotes negative samples with zero quality score, and 0 < y ≤ 1 stands for the positive samples with target IoU score y.

Note that σ = y is the global minimum solution of QFL. It increases the loss when the prediction σ is far from the actual value y (making it a “hard” example), and decreases the loss when the prediction is close to y (a “well-estimated” example).

Distributed Focal Loss:

The relative offset from the bounding box coordinates is taken as a regression target. The regression label y as Dirac delta distribution, where it satisfies

Generally, the integral form used for recovering y is as follows,

Based on the previous understanding, instead of considering the bounding box coordinates as a Dirac delta or Gaussian distribution, we have a general distribution $P(x)$ . Now, given the range of label y with minimum $y_0$ and maximum $y_n$ , we estimate the value of $y^hat$ .

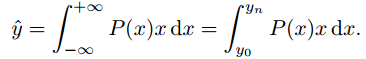
As the same will be used with a Convolutional Neural Network, we convert the integral in a continuous domain into a discrete representation, via changing the range from $y_0, y_n$ , to a set of evenly spaced intervals ${y_0, y_1, y_2, …, y_{n-1}, y_{n}}$ . The estimated regression value can be represented as,

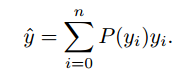
This method allows for a more flexible model that can adapt to any distribution shape without being limited to specific assumptions like those of the Dirac delta or Gaussian distributions. The loss function encourages the value near the label $y$ , by explicitly increasing the probability value of $y_i$ and $y_{i+1}$ . Closely looking at the above equation, it is clear that $\hat{y}$ is represented as a weighted sum of $y_i$ .

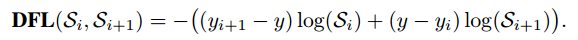
Figure 8: Distribution Focal Loss Equation

Above is the DFL loss, as the learning of the bounding boxes are only for positive samples, so the authors directly used the cross entropy part from the QFL. Here, $S_i$ is a softmax layer with $n+1$ units. $S_i$ represents $P(x)$ . The global minimum solution of DFL, i.e,

yolo loss function python
yolo loss function pytorch
yolo loss function implementation
yolov3 loss function
yolo loss function
loss function in yolo

The final GFL loss is defined as below,

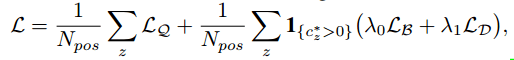
Figure 9: Generalized Focal Loss

Here, $L_Q$ is QFL, and $L_D$ is DFL, and $L_B$ denotes the GIoU Loss, $N_{pos}$ stands for the number of positive samples $\lambda_0$ and $\lambda_1$ are the balance weights for $L_Q$ and $L_D$ , respectively.

💡 You can access the entire codebase and all our other posts by simply subscribing to the blog post, and we’ll send you the link to download link.

Download Code To easily follow along this tutorial, please download code by clicking on the button below. It's FREE!

Click here to download the source code to this post

QFL Pytorch Code Explanation:

import torch
import torch.nn as nn
import torch.nn.functional as F

# Source: https://github.com/gau-nernst/centernet-lightning
# Define the QualityFocalLoss class
class QualityFocalLoss(nn.Module):
    '''Quality Focal Loss. Use logits to improve numerical stability. Generalized Focal Loss: https://arxiv.org/abs/2006.04388
    '''
    def __init__(self, beta: float = 2, reduction: str = 'sum'):
        '''Quality Focal Loss. Default values are from the paper

        Args:
            beta: control the scaling/modulating factor to reduce the impact of easy examples
            reduction: either none, sum, or mean 
        '''

        super().__init__()
        assert reduction in ('none', 'sum', 'mean')
        self.beta = beta
        self.reduction = reduction

    def forward(self, inputs: torch.Tensor, targets: torch.Tensor):
        probs = torch.sigmoid(inputs)
        ce_loss = F.binary_cross_entropy_with_logits(inputs, targets, reduction='none')
        modulating_factor = torch.pow(torch.abs(targets - probs), self.beta)
        loss = modulating_factor * ce_loss
        
        if self.reduction == 'none':
            return loss
        elif self.reduction == 'sum':
            return torch.sum(loss)
        elif self.reduction == 'mean':
            return loss.mean()  # Adjusted to use mean directly for simplicity

# Example inputs
inputs = torch.randn(5, requires_grad=True)  # Example logits for 5 instances
targets = torch.empty(5).random_(2)  # Binary targets for the same instances

# Instantiate QualityFocalLoss and compute loss
quality_focal_loss = QualityFocalLoss(reduction='mean')  # Using 'mean' for illustration
loss_output = quality_focal_loss(inputs, targets)

# Print output loss
print(loss_output) # output:  tensor(0.3341, grad_fn=<MeanBackward0>)

Given the model prediction and targets, we first pass the inputs through the sigmoid function, such that the input values are mapped between 0 and 1. Next, we compute the 2nd part from the formula using the cross entropy function. Then the modulating factor is calculated by taking an absolute difference between the model prediction and targets. Later, both parts are multiplied to get the final loss. self.reduction contains the reduction type, there are different methods for performing reduction, one is sum, one is mean, and sometimes people pass None. The purpose of this is to obtain a single value that represents the loss.

DLF Pytorch Code Explanation:

import torch
import torch.nn as nn
import torch.nn.functional as F

# Source: https://github.com/Yuxiang1995/ICDAR2021_MFD
# Define the distribution_focal_loss function
def distribution_focal_loss(pred, label):
    r"""Distribution Focal Loss (DFL) is from `Generalized Focal Loss: Learning
    Qualified and Distributed Bounding Boxes for Dense Object Detection
    <https://arxiv.org/abs/2006.04388>`_.

    Args:
        pred (torch.Tensor): Predicted general distribution of bounding boxes
            (before softmax) with shape (N, n+1), n is the max value of the
            integral set `{0, ..., n}` in paper.
        label (torch.Tensor): Target distance label for bounding boxes with
            shape (N,).

    Returns:
        torch.Tensor: Loss tensor with shape (N,).
    """
    dis_left = label.long()
    dis_right = dis_left + 1
    weight_left = dis_right.float() - label
    weight_right = label - dis_left.float()
    loss = F.cross_entropy(pred, dis_left, reduction='none') * weight_left \
        + F.cross_entropy(pred, dis_right, reduction='none') * weight_right
    return loss

class DistributionFocalLoss(nn.Module):

    def __init__(self,
                 reduction='mean',
                 loss_weight=1.0):
        super(DistributionFocalLoss, self).__init__()
        self.reduction = reduction
        self.loss_weight = loss_weight

    def forward(self,
                pred,
                target,
                weight=None,
                avg_factor=None,
                reduction_override=None):
        assert reduction_override in (None, 'none', 'mean', 'sum')
        reduction = (
            reduction_override if reduction_override else self.reduction)
        loss_cls = self.loss_weight * distribution_focal_loss(
            pred,
            target)
        loss = loss_cls.mean()
        return loss

# Example inputs
N, n = 5, 10  # Assume N samples and max value n for the integral set
pred = torch.randn(N, n+1, requires_grad=True)  # Random predictions
label = torch.rand(N) * n  # Random target labels in the range [0, n]

# Instantiate DistributionFocalLoss and compute loss
distribution_focal_loss_instance = DistributionFocalLoss()
loss_output = distribution_focal_loss_instance(pred, label)

print(loss_output) # output: tensor(3.5175, grad_fn=<MeanBackward0>)

The given continuous label is discretized into dis_left and dis_right. This turns a continuous regression problem into a classification problem with n+1 classes, where n is the maximum integral value in the target range.

weight_left and weight_right are calculated as the difference between the label and its discretized counterparts, serving as interpolation weights that reflect the contribution of the neighbouring integral values to the actual continuous target.

The loss is computed as a weighted sum of the cross-entropy loss for both the dis_left and dis_right.

The final DFL is multiplied by the loss_weight, generally kept at 1.

Varifocal Loss:

VarifocalNet was first published at CVPR 2021 by Zhang et al. from the University of Queensland. The authors introduced the VarifocalNet or VFNet model with an Iou-aware Classification Score (IACS) named Varifocal Loss as a joint representation of object presence confidence and localization accuracy. Besides that, they also modified the 4-point bounding box to a 9-point star-shaped bounding box for better feature representation. Although the paper has a lot of interesting elements, we will only focus on the Varifocal Loss function.

yolo loss function
Yolo loss function in object detection
yolo loss function explained
yolo v1 loss function
yolo v8 loss function
keras yolo custom loss function
keras yolo loss function
Yolo loss function example
yolo v8 loss function
yolo loss function python
yolo loss function pytorch
yolo loss function implementation
yolov3 loss function

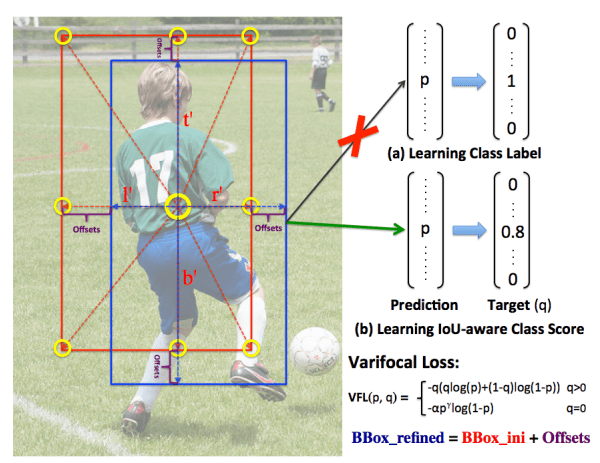
Figure 10: An illustration 9 point star bounding box and the method used in VerifocalNet.

Problems Addressed by Varifocal Loss:

Before proceeding, let’s identify the challenges that highlighted the need for Varifocal Loss, which include:

In object detection, we predict the bounding box and the class of the object inside the bounding box. Regardless of being a one-stage or two-stage, a detection model proposes a lot of bound boxes for each object, called dense prediction. Later NMS is applied on top of these bounding boxes to select the bounding box that fits the object perfectly. Generally, the classification score is used to rank the bounding box in NMS, which is not recognized as an optimal candidate as they are generally considered a bad estimator of the bounding box localization accuracy. This is because an accurately localized detection with a low classification score may be mistakenly removed in NMS.

Existing dense object detectors predict either an additional IoU score or a centerness score as the localization accuracy estimation and multiply them by the classification score to rank detections in NMS.

This is a wrong strategy because multiplying localization accuracy estimation and classification score might result in some sub-optimal representation of the localization estimation, leading to a worse rank basis.

Besides, having a separate branch for localization score prediction incurs an additional computation burden.

Solutions Introduced:

Varifocal Loss is inspired by Focal loss. But in Varifocal loss, negative examples are down-weighted for addressing the problem of class imbalance. On the other hand, it up-weights high-quality positive examples for generating prime directions. This loss function aims to estimate an IoU-Aware classification score that simultaneously represents the classification loss and the localization quality. They need a single loss to give intuition for both, for correctly ranking the dense bounding box predictions.

They utilize the concept of example weighting from focal loss to mitigate the class imbalance problem encountered during training a dense object detector for continuous Intersection-over-Union Aware Classification Score (IACS) regression. However, in contrast to focal loss, which applies the same principle to both positive and negative examples, they apply an asymmetric treatment. Their varifocal loss, which also derives from the binary cross-entropy loss, modifies this approach,

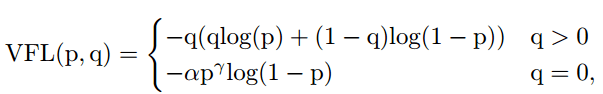
Figure 11: Varifocal Loss Equation

In the given context, p represents the predicted IACS, and q denotes the target score. In the case of a foreground point, the q value for its ground-truth class is established as the Intersection over Union (IoU) between the generated bounding box and its corresponding ground truth (gt IoU). If a point belongs to the background, the target q for all classes is uniformly set to 0.

The above equation illustrates that the varifocal loss specifically diminishes the loss impact originating from negative examples $(q=0)$ by adjusting their losses through a factor of $p^{\gamma}$ . Positive examples $(q \ge 0)$ , on the other hand, are not similarly de-emphasized. This lack of down-weighting for positive examples is due to their scarcity in comparison to negatives, and they should retain their valuable learning signals.

Pytorch Code explanation:

import torch
import torch.nn as nn
import torch.nn.functional as F
from typing import Optional


# Source: https://github.com/hyz-xmaster/VarifocalNet
def varifocal_loss(
    logits: torch.Tensor,
    labels: torch.Tensor,
    weight: Optional[torch.Tensor]=None,
    alpha: float=0.75,
    gamma: float=2.0,
    iou_weighted: bool=True,
):
    
    """`Varifocal Loss <https://arxiv.org/abs/2008.13367>`

    Args:
        logits (torch.Tensor): The model predicted logits with shape (N, C), 
        C is the number of classes
        labels (torch.Tensor): The learning target of the iou-aware
            classification score with shape (N, C), C is the number of classes.
        weight (torch.Tensor, optional): The weight of loss for each
            prediction. Defaults to None.
        alpha (float, optional): A balance factor for the negative part of
            Varifocal Loss, which is different from the alpha of Focal Loss.
            Defaults to 0.75.
        gamma (float, optional): The gamma for calculating the modulating
            factor. Defaults to 2.0.
        iou_weighted (bool, optional): Whether to weight the loss of the
            positive example with the iou target. Defaults to True.
    """
    assert logits.size() == labels.size()
    logits_prob = logits.sigmoid()
    labels = labels.type_as(logits)
    if iou_weighted:
        focal_weight = labels * (labels > 0.0).float() + \
            alpha * (logits_prob - labels).abs().pow(gamma) * \
            (labels <= 0.0).float()

    else:
        focal_weight = (labels > 0.0).float() + \
            alpha * (logits_prob - labels).abs().pow(gamma) * \
            (labels <= 0.0).float()

    loss = F.binary_cross_entropy_with_logits(
        logits, labels, reduction='none') * focal_weight
    loss = loss * weight if weight is not None else loss
    return loss



class VariFocalLoss(nn.Module):
    def __init__(
        self,
        alpha: float=0.75,
        gamma: float=2.0,
        iou_weighted: bool=True,
        reduction: str='mean',
    ):
        # VariFocal Implementation: https://github.com/hyz-xmaster/VarifocalNet/blob/master/mmdet/models/losses/varifocal_loss.py
        super(VariFocalLoss, self).__init__()
        assert reduction in ('mean', 'sum', 'none')
        assert alpha >= 0.0
        self.alpha = alpha
        self.gamma = gamma
        self.iou_weighted = iou_weighted
        self.reduction = reduction

    def forward(self, logits, labels):
        loss = varifocal_loss(logits, labels, self.alpha, self.gamma, self.iou_weighted)

        if self.reduction == 'sum':
            return loss.sum()
        elif self.reduction == 'mean':
            return loss.mean()
        else:
            return loss


N, C = 5, 4  # Number of samples N and number of classes C
logits = torch.randn(N, C, requires_grad=True)  # Example logits
labels = torch.rand(N, C)  # Example labels, assuming continuous values for demonstration


# Recompute the loss with everything correctly defined
vari_focal_loss_instance = VariFocalLoss()
loss_output_corrected = vari_focal_loss_instance(logits, labels)

# Print the corrected loss output
print(loss_output_corrected) # output tensor(0.2350, grad_fn=<MeanBackward0>)

logits_prob = logits.sigmoid() converts the logits to probabilities using the sigmoid function, corresponding to the predicted probability $p$ in the varifocal loss formula.

Let’s break down if iou_weighted part, in the formula, the scaling factor is multiplied by the cross entropy part, for $q = 0$ , it is $-\alpha p^{\gamma}$ and for $q>0$ it is $-q$ . Here, the part

signifies the same, but in a hybrid function fashion. It uses the IoU scores directly as weights for the positive labels and negative labels, it calculates $-\alpha p^{\gamma}$ . Later we calculate F.binary_cross_entropy_with_logits and multiply the focal_weight with the loss. Later another weight value is multiplied with the loss; generally, it’s given with the loss to manage its contribution to the training. If used with an auxiliary loss, usually, it’s kept as None. In the forward function, we use the varifocal_loss function and then a reduction method.

Key Takeaways

Generalized Approach to Loss Functions: The article highlights the innovation behind Generalized Focal Loss (GFL) and Varifocal Loss, emphasizing their role in addressing specific object detection challenges, thereby showcasing the evolution of loss functions in enhancing YOLO model performance.
Integration of Localization and Classification: A key design choice in GFL is the joint representation of localization quality and classification score, a novel approach that strengthens the correlation between these two critical aspects of object detection, leading to more accurate and reliable detection outcomes.
Continuous Variant of Focal Loss: The article explains how GFL adapt the Focal Loss concept to support continuous labels, addressing the challenge of class imbalance with a refined focus on high-quality object detection.
Probabilistic Approach to Object Detection: Emphasizing a probabilistic viewpoint, these loss functions account for the inherent uncertainty and ambiguity in real-world data, advocating for a more flexible and adaptive model of bounding box prediction.
Practical Implementation with PyTorch: Providing PyTorch code implementations, the article bridges theoretical concepts with practical application, encouraging readers to experiment with these loss functions in their own YOLO model implementations.
Optimization of IoU-Aware Classification via Varifocal Loss: Varifocal Loss is intricately designed to refine object detection by optimizing the IoU-aware classification score, thereby enabling a more accurate and discriminating ranking of detection boxes. This loss function distinctively modifies the conventional approach by asymmetrically treating positive and negative examples, significantly reducing the misclassification of accurately localized detections as background.

Conclusion

Through this article, we understand the design choices of these loss functions, how a continuous variant of focal loss is introduced, how class imbalance problems are handled, how uncertainty is handled by taking a probabilistic approach, the importance of localization quality estimation, etc. Object detection is a delicate task, one needs to keep an eye on every minute detail in order to make it work in a generalized fashion. We hope these two articles gave a good sense of deep learning loss formulation and implementation. We encourage everyone to read the papers associated with the loss functions, as they will give more in-depth knowledge about the work and use this article as a reference material. Please leave a comment if you face any issues understanding the article.