A conventional video or picture captures the three-dimensional world in two dimensions, losing crucial information regarding depth, which many applications now demand. Depth estimation is a challenging problem, and there have been efforts to solve this problem.
The most popular setup, called Stereo Vision, uses a pair of cameras, finds corresponding points in the two cameras, and estimates the depth based on disparity. More recently, Deep Learning based methods have been used to estimate disparity from a stereo pair of images.
In this post, we will discuss some of them.
This post is part of our series on Introduction to Spatial AI, which consists of the following articles :
- Introduction to Epipolar Geometry and Stereo Vision
- Making a Low-Cost Stereo Camera Using OpenCV
- Depth Estimation Using Stereo Camera and OpenCV
- Disparity Map Estimation Using Deep Learning
- More to come
- Classical approach to Disparity Estimation
- Deep Learning-Based Approaches for Disparity Estimation
- Studying the PSMNet Architecture
- Evaluating Performance of Stereo-Matching Networks
- Summary
Classical Approach to Disparity Estimation
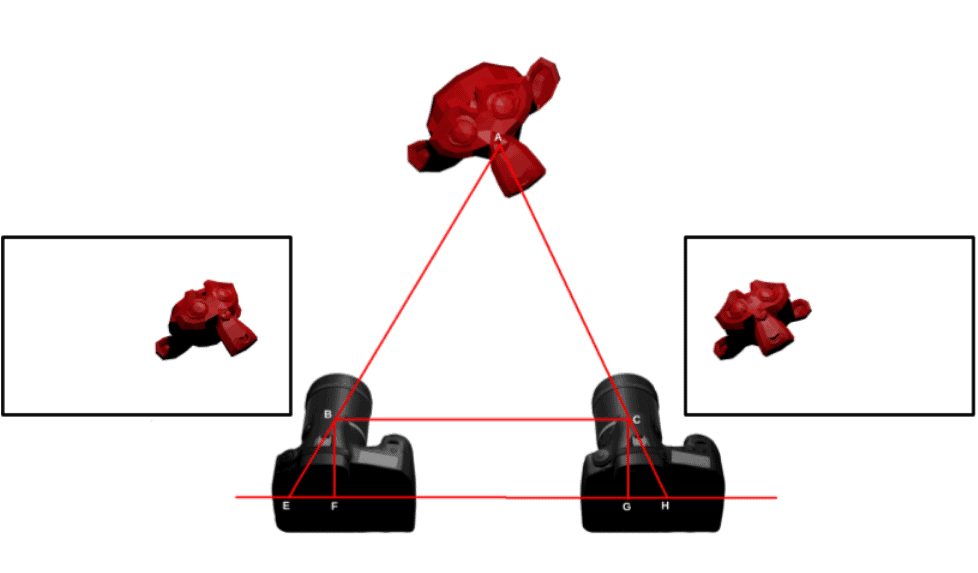
Image Stereo Images from Stereo Camera setup
The classical method to find a disparity map for a pair of rectified stereo images uses the stereo-matching technique. This technique computes correspondence between the pixels of the left and right image, by comparing the pixel-neighborhood information for both images. Using a stereo pair, the disparity map is obtained. For a detailed explanation on how to get the depth map from the disparity map, please go through our previous Depth Estimation, Using Stereo Camera and OpenCV post.
Deep Learning-Based Approaches for Disparity Estimation
Using the Dataset
A good dataset is the backbone of any solution that’s based on Deep Learning, and the same is true even for depth estimation.
The most popular stereo dataset is called KITTI. Some other useful datasets are SceneFlow, Middlebury, and Holopix50K.
KITTI Datasets
A project of Karlsruhe Institute of Technology and the Toyota Technological Institute, KITTI has set up a suite of sensors on cars that collect rich data for autonomous-driving cars. The sensor suite consists of
- Colored and gray channel stereo cameras
- A Velodyne-laser scanner, which provides accurate 3D information, in the form of raw point clouds
- A GPS-localization system
KITTI 2012
KITTI 2012, introduced in CVPR2012, is a stereo dataset consisting of static scenes captured with a stereo camera setup.
KITTI 2015
KITTI 2015, introduced in CVPR2015, is a stereo dataset with dynamic objects in the scene.
This post will focus on the KITTI 2015 Dataset.
Using Networks for Disparity Estimation:
We want to estimate the disparity from a stereo pair of rectified images, by dense-stereo matches. This can also be done by Deep Learning-based models. One of the initial solutions was Matching Cost Convolutional Neural Networks (MC-CNN). Many more methods followed..
Two of the widely experimented ways are
Direct Regression Methods
Direct regression methods try to estimate the per-pixel disparity from the input images directly without taking into account the geometric constraints in stereo matching. This is a fully data-driven approach that utilizes large U-shaped 2D-convolution networks. Not accounting for geometric constraints however places them behind volumetric methods, when it comes to performance.
Volumetric Methods
Volumetric methods leverage the concept of semi-global matching and build a 4D-feature volume, by concatenating features from each disparity shift. It has four major components:
- A feature net to extract features from the input images
- A cost-volume module to concatenate the features extracted from the left and right images
- A matching net to compute matching costs from the 4D-feature volume with 3D convolutions
- The regression module to regress disparity
We will look at the most famous volumetric method for disparity estimation, the Pyramid Stereo Matching Network (PSMNet). While PSMNet is not the state-of-the-art network for stereo matching, most of the networks proposed for stereo matching in volumetric methods are inspired by PSMNet. That makes it a great starting point for network-based stereo matching. So let’s examine the architecture of PSMNet:

The architecture of PSMNet showing its different modules
2D Feature Matching
The Convolutional Neural Network (CNN) helps extract features from the images, which can be edges or textures across the image. In PSMNet,
- CNN gives out the feature map, which is ¼ the input image size and summarizes the detected features in the input.
- Applied to both the input images, these CNNs share the same weights, so that similar features are extracted from both the images, which as you will see is important for the following steps.
Here’s the code for 2D feature matching:
# importing modules
import torch
import torch.nn as nn
import numpy as np
# define nn.Sequential for convenience
def convbn(in_planes, out_planes, kernel_size, stride, pad, dilation):
return nn.Sequential(nn.Conv2D(in_planes, out_planes, kernel_size=kernel_size, stride=stride, padding=dilation if dilation>1 else pad, dilation=dilation, bias=False),
nn.BatchNorm2d(outplanes))
# define Basic Block
class BasicBlock(nn.modules):
expansion = 1
def __init__(self, inplanes, stride, downsample, pad, dilation):
super(BasicBlock, self).__init__()
self.conv1 = nn.Sequential(convbn(inplanes, planes, 3, stride, pad, dilation),
nn.ReLU(inplace=True))
self.conv2 = convbn(planes, planes, 3, 1, pad, dilation)
self.downsample = downsample
self.stride = stride
def forward(self, x):
out = self.conv1(x)
out = self.conv2(out)
if self.downsample is not None:
x = self.downsample(x)
out += x
return out
# Define the 2D Feature Extraction Module
class CNN_2D(nn.Module):
def __init__(self):
super(CNN_2D, self).__init__()
self.inplaces = 32
self.firstconv = nn.Sequential(convbn(3, 32, 3, 2, 1, 1),
nn.ReLU(inplace=True),
convbn(32, 32, 3, 1, 1, 1),
nn.ReLU(inplace=True),
convbn(32, 32, 3, 1, 1, 1),
nn.ReLU(inplace=True))
self.layer1 = self._make_layer(BasicBlock, 32, 3, 1, 1, 1)
self.layer2 = self._make_layer(BasicBlock, 64, 16, 2, 1, 1)
self.layer3 = self._make_layer(BasicBlock, 128, 3, 1, 1, 1)
self.layer4 = self._make_layer(BasicBlock, 128, 3, 1, 1, 2)
def _make_layer(self, block, planes, blocks, stride, pad, dilation):
downsample = None
if(stride!=1 or self.inplanes != planes * block.expansion):
downsample = nn.Sequential(nn.Conv2d(self.inplanes, planes*block.expansion,
kernel_size=1, stride=stride,
bias=False),
nn.BatchNorm2d(planes*block.expansion))
layers = []
layers.append(block(self.inplanes, planes, stride, downsample, pad, dilation))
self.inplanes = planes * block.expansion
for i in range(1, blocks):
layers.append(block(self.inplanes, planes, 1, None, pad, dilation))
return nn.Sequential(*layers)
def forward(self, x):
output = self.firstconv(x)
output = self.layer1(output)
output_raw = self.layer2(output)
output = self.layer3(output_raw)
output_skip = self.layer4(output)
return ouput_skip
SPP Module :
The SPP (Spatial Pyramid Pooling) module extracts the feature map of different scales. The following figure explains the SPP module in detail.
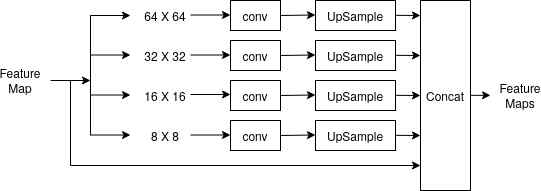
Diagram explaining SPP Module to extract feature maps at various scales
In the SPP module,
- To get contextual information at various scales, the feature maps are filtered through average-pooling filters of four different resolutions:
- 64X64
- 32X32
- 16X16
- 8X8
- Then these maps are passed through a 1X1 convolution layer to reduce the dimensions.
- Next, the maps are upsampled to match the size of the original feature map
- Finally, these maps are concatenated along with the original feature map.
Let’s look at the code for the SPP module:
# define SPP Module
class SPP_Module(nn.Module):
def __init__(self):
super(SPP_Module, self).__init__()
# define the 4 filters and other convolutional layers
self.branch1 =nn.Sequential(nn.AvgPool2d(64,64), stride=(64,64),
convbn(128,32,1,1,0,1),
nn.ReLU(inplace=True))
self.branch2 =nn.Sequential(nn.AvgPool2d(32,32), stride=(32,32),
convbn(128,32,1,1,0,1),
nn.ReLU(inplace=True))
self.branch3 =nn.Sequential(nn.AvgPool2d(16,16), stride=(16,16),
convbn(128,32,1,1,0,1),
nn.ReLU(inplace=True))
self.branch4 =nn.Sequential(nn.AvgPool2d(8,8), stride=(8,8),
convbn(128,32,1,1,0,1),
nn.ReLU(inplace=True))
self.lastconv =nn.Sequential(convbn(320,128,3,1,1,1),
nn.ReLU(inplace=True),
nn.conv2d(128,32,kernel_size=1,
padding=0,
stride=1,
bias=False))
def forward(self, x):
# code for branching of SPP module
op1 = self.branch1(x)
op1 =F.upsample(op1,(x.size()[2],x.size()[3]),mode='bilinear')
op2 = self.branch1(x)
op2 = F.upsample(op2,(x.size()[2],x.size()[3]),mode='bilinear')
op3 = self.branch1(x)
op3 = F.upsample(op3,(x.size()[2],x.size()[3]),mode='bilinear')
op4 = self.branch1(x)
op4 = F.upsample(op4,(x.size()[2],x.size()[3]),mode='bilinear')
op_concat = torch.cat((x, op4,op3,op2,op1),1)
op_concat = self.lastconv(op_concat)
return op_concat
Cost Volume :
After getting the feature maps from various scales, we want to combine the features from the images on the left as well as right. The Cost Volume Module then:
- Concatenates the features extracted from the left and right images
- Stores the distance between the features
This results in a 4D array of size: height × width × (max disparity + 1) × (feature sizes), which is called Cost Volume.
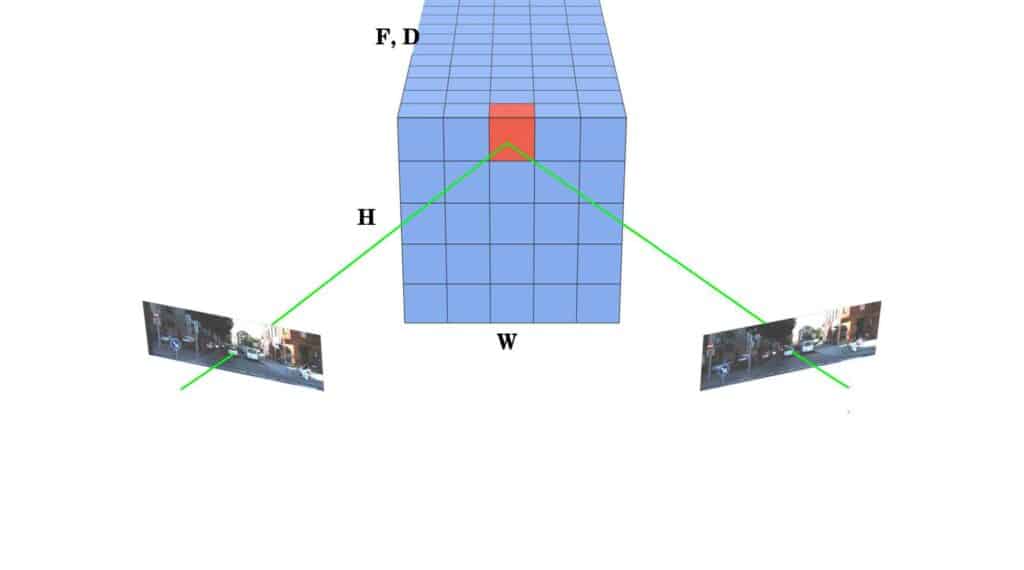
Diagram showing how the cost volume is constructed
Each voxel of the cost volume is the matching cost of corresponding features, projected from the left and right views. Computing the cost volume requires much calculation and memory. To know various cost-volume techniques, refer to this study. It also provides an optimized method for doing cost-volume estimation, which produces ‘dense’ 3d-cost volumes. Okay, let’s not linger more with the concept and check out the code for finding cost volume in PSMNet.
# import modules
import torch
from torch.autograd import Variable
# define the Cost Volume Module
cost = Variable(torch(FloatTensor(left_img_ftrs.size()[0],
left_img_ftrs.size()[1]*2,
maxDisparity // 4,
left_img_ftrs.size()[2],
left_img_ftrs.size()[3]).zero_()))
# concatenate the features in cost volume
for i in range(self.maxdisp//4):
if(i>0):
cost[:,:left_img_ftrs.size()[1],i,:,i:] = left_img_ftrs[:,:,:1:]
cost[:,left_img_ftrs.size()[1]:,i,:,i:] = rght_img_ftrs[:,:,::-i]
else:
cost[:,:left_img_ftrs.size()[1],i,:,i:] = left_img_ftrs
cost[:,left_img_ftrs.size()[1]:,i,:,i:] = rght_img_ftrs
cost = cost.contiguous()
3D CNN and Regression Module
From the Cost Volume Module, we get the 4D-cost volume, and now we want to concatenate the information, along the two dimensions:
- disparity dimension (3rd dimension in 4D-cost volume)
- spatial dimension (4th dimension of 4D cost volume)
To do this, we use the 3D CNN. PSMNet has two variations of 3D CNN architectures:
- The first one is a basic architecture that uses 12 3x3x3 convolution layers, with skip connections, as shown below:

Network Diagram of Basic 3D CNN Module
Have a look at its code too:
# the 3D Feature matching module
class CNN_3D_basic(nn.Module):
def __init__(self):
super(CNN_3D_basic, self).__init__()
# define layers for 3D Feature matching module
self.dres0 = nn.Sequential(convbn_3d(64, 32, 3, 1, 1),
nn.ReLU(inplace=True),
convbn_3d(32, 32, 3, 1, 1),
nn.ReLU(inplace=True))
self.dres1 = nn.Sequential(convbn_3d(32, 32, 3, 1, 1),
nn.ReLU(inplace=True),
convbn_3d(32, 32, 3, 1, 1))
self.dres2 = nn.Sequential(convbn_3d(32, 32, 3, 1, 1),
nn.ReLU(inplace=True),
convbn_3d(32, 32, 3, 1, 1))
self.dres3 = nn.Sequential(convbn_3d(32, 32, 3, 1, 1),
nn.ReLU(inplace=True),
convbn_3d(32, 32, 3, 1, 1))
self.dres4 = nn.Sequential(convbn_3d(32, 32, 3, 1, 1),
nn.ReLU(inplace=True),
convbn_3d(32, 32, 3, 1, 1))
self.dres5 = nn.sequential(convbn_3d(32, 32, 3, 1, 1),
nn.ReLU(inplace=True),
nn.Conv3d(32,1,kernel_size=3,
padding=1,
stride=1,
bias=False))
def forward(self, cost_4D):
# combine all the layers to make the 3D Feature matching net
cost0 = self.dres0(cost_4D)
cost0 = self.dres1(cost0) + cost0
cost0 = self.dres2(cost0) + cost0
cost0 = self.dres3(cost0) + cost0
cost0 = self.dres4(cost0) + cost0
cost = self.dres5(cost0)
return cost
2. Because the basic architecture cannot exploit the contextual information, the PSMNet also has an Encoder-Decoder based architecture variant called the stacked-hourglass architecture.
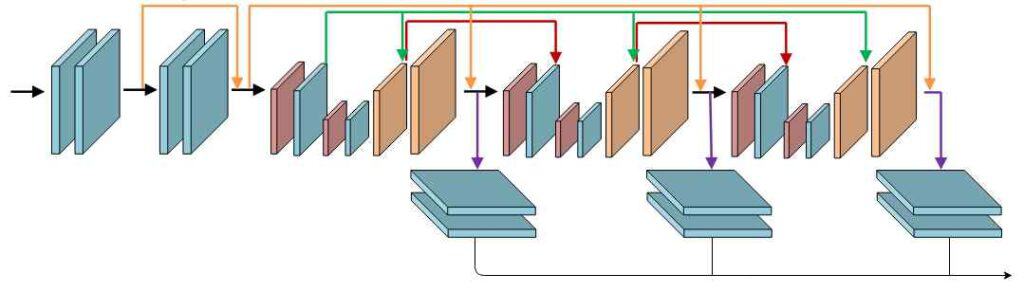
Network Architecture of stacked hourglass variant of 3D CNN Module
Next, examine its code:
# Import modules
import torch.nn as nn
import torch.nn.functional as F
def convbn_3d(in_planes, out_planes, kernel_size, stride, pad):
return nn.Sequential(nn.Conv2D(in_planes, out_planes, kernel_size=kernel_size, padding=pad, stride=stride, bias = False), nn.BatchNorm2d(outplanes))
# define the hourglass structures for stacked hourglass architecture
class hourglass(nn.Module):
def __init__(self, inplanes):
super(hourglass, self).__init__()
# define the layers for hourglass
self.conv1 = nn.Sequential(convbn_3d(inplanes, inplanes*2,
kernel_size=3,
stride=1, pad=1),
nn.ReLU(inplace=True))
self.conv2 = convbn_3d(inplanes, inplanes*2, kernel_size=3,
stride=1, pad=1)
self.conv3 = nn.Sequential(convbn_3d(inplanes*2, inplanes*2,
kernel_size=3,
stride=2, pad=1),
nn.ReLU(inplace=True))
self.conv4 = nn.Sequential(convbn_3d(inplanes*2, inplanes*2,
kernel_size=3,
stride=2, pad=1),
nn.ReLU(inplace=True))
self.conv5 = nn.Sequential(nn.convTranspose3d(inplanes*2,
inplanes*2,
kernel_size=3,
stride=2, padding=1,
output_padding=1,
bias=False),
nn.BatchNorm3d(inplanes*2))
self.conv6 = nn.Sequential(nn.convTranspose3d(inplanes*2,
inplanes,
kernel_size=3,
stride=2, padding=1,
output_padding=1,
bias=False),
nn.BatchNorm3d(inplanes))
def forward(self, x, out, pre_skip, post_skip):
# combine all the layers to make the hourglass structures
out = self.conv1(x)
pre = self.conv2(out)
if(post_skip is not None):
pre = pre + post_skip
pre = F.relu(pre, inplace=True)
out = self.conv3(pre)
out = self.conv4(pre)
post = self.conv5(out)
if(pre_skip is not a look at its code too: None):
post = post + pre_skip
else:
post = post + pre
post = F.relu(post, inplace=True)
out = self.conv6(post)
return out, pre, post
# Disparity regression module
class disparityregression(nn.Module):
def __init__(self, maxdisp):
super(disparityregression, self).__init__()
self.disp = torch.Tensor(np.reshape(np.array(range(maxdisp)),
[1, maxdisp,1,1]))
def forward(self, x):
out = torch.sum(x*self.disp.data,1,keepdim=True)
return out
# define stacked hourglass module
class CNN_3D_hourglass(nn.Module):
def __init__(self, maxdisp):
self.maxdisp = maxdisp
super(CNN_3D_hourglass, self).init()
# define the layers for stacked hourglass module
self.dres0 = nn.Sequential(convbn_3d(64, 32, 3, 1, 1),
nn.ReLU(inplace=True),
convbn_3d(32, 32, 3, 1, 1),
nn.ReLU(inplace=True))
self.dres1 = nn.Sequential(convbn_3d(32, 32, 3, 1, 1),
nn.ReLU(inplace=True),
convbn_3d(32, 32, 3, 1, 1))
# use the hourglass modules created
self.dres2 = hourglass(32)
self.dres3 = hourglass(32)
self.dres4 = hourglass(32)
self.dres5 = nn.sequential(convbn_3d(32, 32, 3, 1, 1),
nn.ReLU(inplace=True),
nn.Conv3d(32,1,kernel_size=3,
padding=1,
stride=1,
bias=False))
self.dres6 = nn.sequential(convbn_3d(32, 32, 3, 1, 1),
nn.ReLU(inplace=True),
nn.Conv3d(32,1,kernel_size=3,
padding=1,
stride=1,
bias=False))
self.dres7 = nn.sequential(convbn_3d(32, 32, 3, 1, 1),
nn.ReLU(inplace=True),
nn.Conv3d(32,1,kernel_size=3,
padding=1,
stride=1,
bias=False))
def forward(self, cost):
# combine the layers to form the stacked hourglass module
cost0 = self.dres0(cost)
cost0 = self.dres1(cost0) + cost0
out1, pre1, post1 = self.dres2(cost0, None, None)
out1 = out1 + cost0
out2, pre2, post2 = self.dres3(out1, pre1, post1)
out2 = out2 + cost0
out3, pre3, post3 = self.dres4(out2, pre2, post2)
out3 = out3 + cost0
cost1 = self.dres4(out1)
cost2 = self.dres5(out2) + cost1
cost3 = self.dres5(out3) + cost2
cost3 = F.upsample(cost3, [self.maxdisp, left.size()[2],
left.size()[3]], mode='trilinear')
cost3 = torch.squeeze(cost3, 1)
pred3 = F.softmax(cost3, dim=1)
# also add the disparityregression module
pred3 = disparityregression(self.maxdisp)(pred3)
return pred3
- The output of 3D CNN is upsampled to the size of height x width x (max disparity + 1) by Interpolation. Trilinear interpolation is an upsampling method, which uses a distance-weighted average, of the nearest cell’s 3D features, to obtain the value of the newly-made cells.
- After interpolation, we have a 3D-cost volume, height x width x (max disparity + 1), which has (max disparity + 1) disparity images of size height x width.
- The probability along the disparity dimension is normalized, using the softmax operation.
- The normalized probability values are multiplied with the disparity to obtain the final disparity.
Keep in mind that the softmax is a logistic-regression function, and it is usually the last activation function used to normalize the output of the network, over a probability distribution. Its mathematical formula is:
![]()
This softmax is plugged into the weighted-disparity formula to get the disparity of the pixel, which is:
![]()
Softmax is a widely-studied function for networks and therefore has all the desired properties for network training like:
- it is differentiable to backpropagate
- is not discrete, hence produces smooth disparities
- And finally, for the training part of the network, a loss function is needed to backpropagate the prediction error. A Smooth L1 loss is used over the L2 loss due to its wide acceptance in similar tasks. The Smooth L1 Loss for PSMNet looks like this:
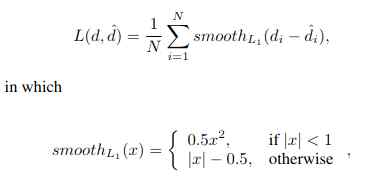
The regression function outputs the final disparity map of the two input images, which however still needs to be converted to a depth map. The depth value is inversely proportional to the disparity values. For a detailed explanation of how to get the depth map from the disparity map, please go back to our Depth Estimation post.
Get the full code for training and testing PSMNet at their Official Code Repository. We have also created a collab notebook to let you play around with the code.
Here are some sample inputs(Left Image) and their respective disparity images.
Sample 1

Example RGB Image(1)

Example Estimated Disparity Image (1)
Sample 2

Example RGB Image (2)

Example Estimated Disparity Image (2)
Evaluating Performance of Stereo-Matching Networks:
Stereo vision being a very important problem in the computer vision domain, there have been a lot of studies revolving on how to improve the output of neural network-based depth estimation. KITTI has this leaderboard, where it shows the submissions and their respective errors.
Check out this KITTI leaderboard of mid-June 2021 on the KITTI 2015 benchmark!
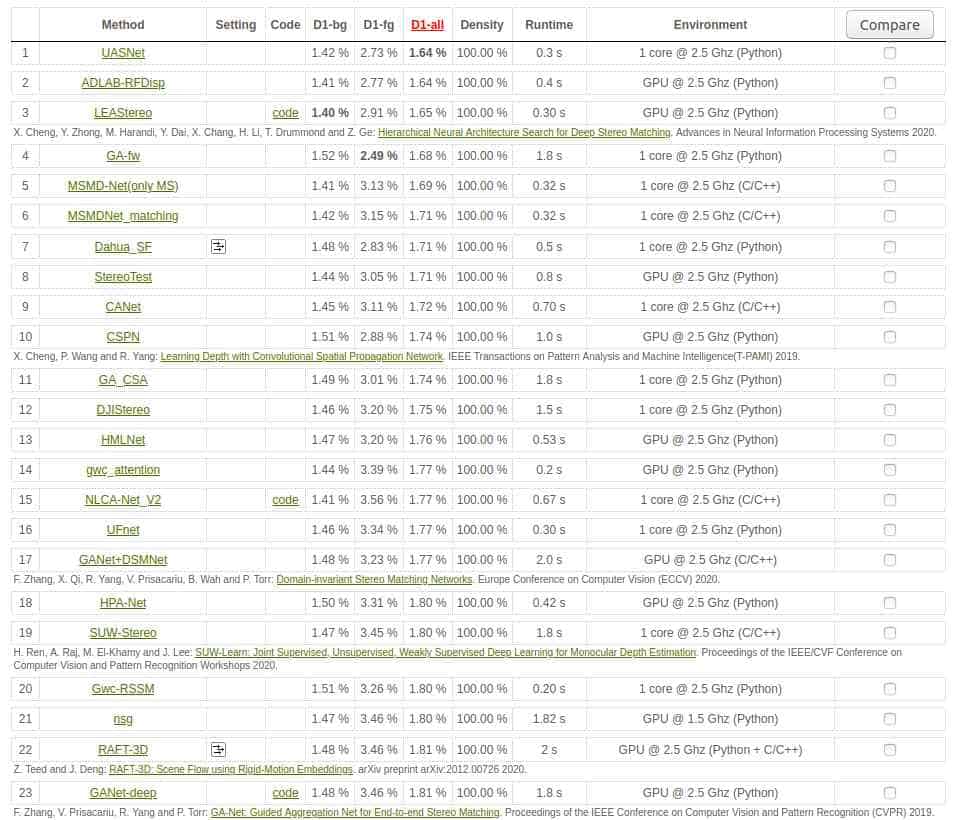
Leaderboard Kitti Stereo Benchmark
PSMNet is ranked 140 on this leaderboard. We can clearly see it’s not the best performer, why is PSMNet important then? The answer remains the same but a lot of stereo vision-based networks in the leaderboard are based on PSMNet, and they mostly reduce the errors, by changing the architecture of the CNN. One interesting method proposed along the same lines, LEAStereo is currently ranked at the top of the leaderboard.
Most of the Volumetric Method architectures have a pipeline that looks like this:

General Overview of Volumetric Disparity Estimation Networks
It contains 4 major modules, in which the modules of PSMNet can be easily merged.
- First, the CNN module along with the SPP module can be placed in the 2D-Feature Extractor module
- Then the Cost Volume module from PSMNet can be mapped directly to the Cost Volume Maker
- Similarly, PSMNet’s 3D-CNN module can be mapped to the 3D-CNN module
- Also, regressor can be mapped to Disparity Regressor.
If we look closely at these modules, only 2 of them are trainable:
- The 2D feature extractor
- And the 3D CNN module
Like we told you above, the networks simply tweak the architecture of these trainable modules for better results. PSMNet itself presented two architectures for the 3D-CNN module. Top-ranker, LEAStereo too follows the same line and applies Neural Architecture Search (NAS) on these modules to reduce error.
Now, what is NAS? Used to automate the designing of neural networks, NAS has recently gained traction because it has been outperforming many of the human-designed networks in various domains, including computer vision.
LEAStereo reduces error by applying Neural Architecture Search (NAS) to zero onto the best network for:
- 2D-feature extractor
- and also 3D CNN
By substituting these networks in the pipeline, LEAStereo completes the whole stereo image to the disparity image network. Find more about LEAStereo and problem formulation, here.
Reducing the error, however, is not enough. The performance of a Stereo-Matching Network is judged on two major grounds:
- Error in depth map
- Time taken to get the inferences from networks
Now, which aspect should you consider when selecting the method for depth estimation for an application? Well, that will depend on the type of application.
- In automatic driving, which is one of the most important stereo-imaging applications, time is a very critical aspect. Most networks can produce inferences in 0.3s, i.e., approx 3 frames per second. But that’s not enough for this driving application.
- There are applications though where time is not a very crucial factor. For example, the bokeh effect estimated by the smartphone camera requires depth maps of extreme accuracy, in order to clearly distinguish between the foreground and background. Only then can it ensure even the tiniest of the hairs come in the foreground. Similar clear cut distinction between the foreground and background is not required in the driving application though. It’s ok if the depth maps are not very accurate, as long as they infer at a good speed.
Summary
Fourth in our Introduction to Spatial AI series, this post discussed neural network-based methods for stereo matching, using a Stereo Camera. With applications increasingly calling for depth information, we looked for solutions, as videos and pictures generally tend to lose depth information.
We saw
- We started with the classical approach that used a stereo pair to obtain a disparity map. Then jumped to the Deep Learning part for stereo matching. We not only introduced some standard datasets for stereo vision, but also focused on KITTI, emphasizing why it is the most famous dataset and benchmark for vision-related tasks.
- Next, we discussed the two network-based methods for getting the disparity from stereo images. One, directly regressing the disparity, and the other a volumetric-based method
- You saw how considering geometric constraints led to better results, making the volumetric-based method our bestbet.
- You then delved deep into the working of one of the most widely accepted networks, the PSMNet. Discussed in detail how the disparity is estimated from PSMNet, including the roles of the SPP module, the cost volume and the 3D CNN and regression module.We also discussed the KITTI leaderboard and saw how the pipeline for the architecture of the volumetric method looks like. You learnt about LEAStereo, which uses NAS to reduce error and find the best suitable network for the two trainable modules in the volumetric-based stereo-matching pipeline.
- And finally, you concluded that when it comes to selecting the method for depth estimation, reducing the error is not enough, time taken for inference also needs to be considered for particular applications.
References
[1] PSMNet : Chang, Jia-Ren and Chen, Yong-Sheng. Pyramid Stereo Matching Network, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018
[2] LEANet : Cheng, Xuelian and Zhong, Yiran and Harandi, Mehrtash and Dai, Yuchao and Chang, Xiaojun and Li, Hongdong and Drummond, Tom and Ge, Zongyuan. Hierarchical Neural Architecture Search for Deep Stereo Matching
[3] MC-CNN : J. Zbontar and Y. LeCun. Stereo matching by training a convolutional neural network to compare image patches. Journal of Machine Learning Research, 17(1-32):2, 2016
[4] GCNet : A. Kendall, H. Martirosyan, S. Dasgupta, P. Henry,R. Kennedy, A. Bachrach, and A. Bry. End-to-end learning of geometry and context for deep stereo regression. In The IEEE International Conference on Computer Vision (ICCV), Oct 2017








100K+ Learners
Join Free OpenCV Bootcamp3 Hours of Learning