SimSiam holds an eminent status in Self-Supervised Learning by simplifying Representation Learning without relying on negative pairs – typically employed in SimCLR to contrast between dissimilar representations and enforce separation in the learned feature space, and also foregoes the reliance on momentum encoder – as used in methods like BYOL. Built on the principles of Contrastive Learning, it offers a streamlined framework with fewer dependencies. By employing an asymmetric architecture and a stop-gradient mechanism (both explained later in this article), SimSiam effectively reduces computational overhead and architectural complexity while maintaining competitive performance, making SimSiam an attractive choice for advancing self-supervised learning frameworks.
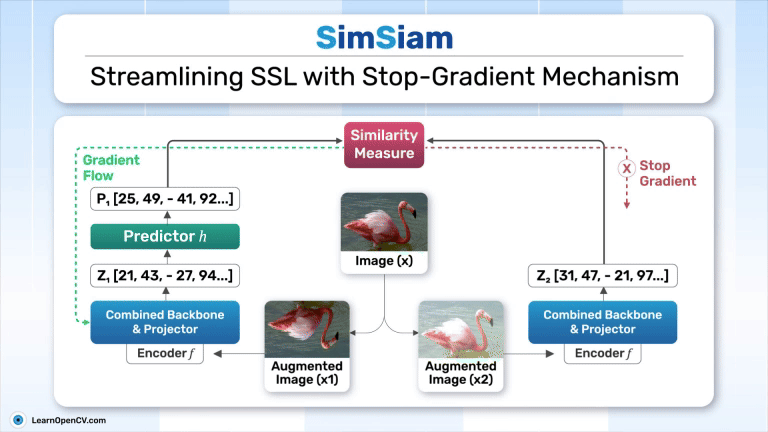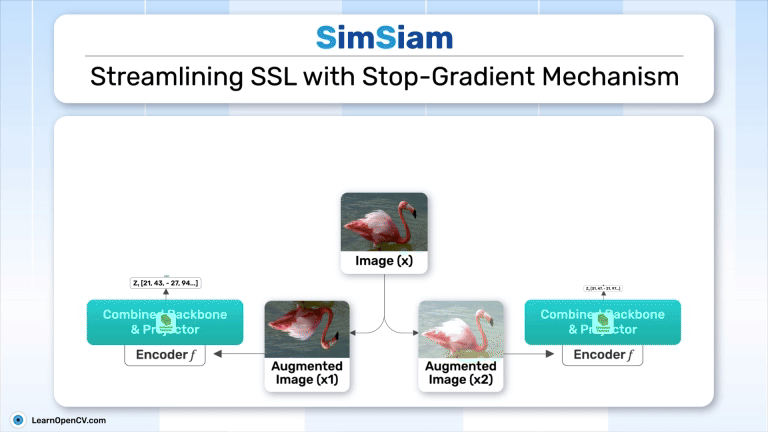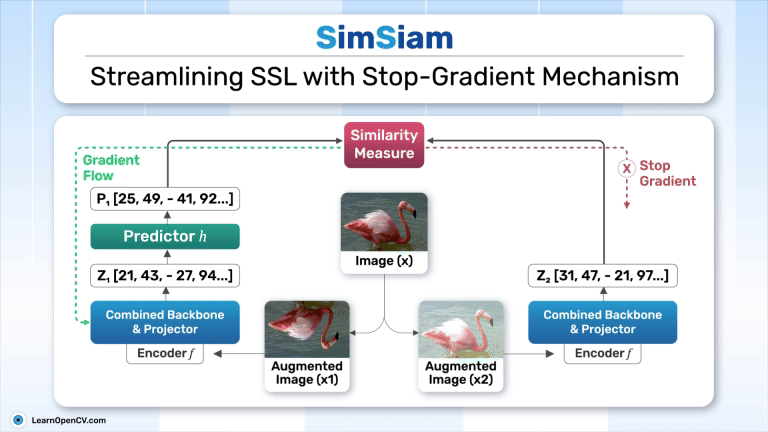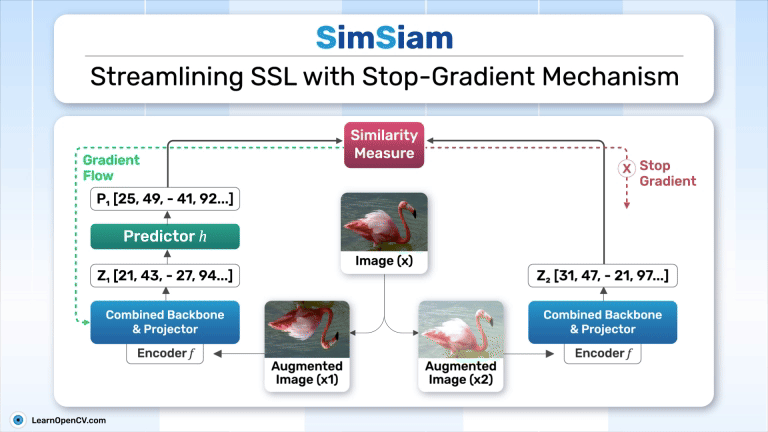
SimSiam, like BYOL and SimCLR, employs a dual-branch architecture with one branch for the online (student network) and another for the target (teacher network), as discussed in one of our previous articles. While the student-teacher framework influences both BYOL and SimSiam, their designs diverge significantly. BYOL incorporates a momentum encoder in its teacher branch to ensure stability for the student branch, adhering closely to the traditional student-teacher paradigm. In contrast, SimSiam eliminates the explicit teacher network, using a stop-gradient mechanism in its target branch to mimic stability.
This blog post delves into SimSiam’s architecture, its innovative pretraining approach, and the practical implementation of fine-tuning SimSiam’s learned representations for downstream tasks, including the implementation codes. Therefore the blog post has been structured as follows –
- Generalized Architecture for SSL Frameworks
- Siamese Networks
- Output Collapse
- SSL General Workflow
- SimSiam (Simple Siamese Networks)
- Key Features of the SimSiam Framework’s Algorithm
- Investigating SimSiam’s Non-Collapsing Dynamics
- Understanding SimSiam’s Implicit Optimization Dynamics
- Extended Insights
- Conclusion
- References
Generalized Architecture for SSL Frameworks
Siamese networks (first introduced in the early 1990s by Bromley and LeCun to solve signature verification as an image matching problem (Bromley et al., 1993)) form the backbone of self-supervised learning frameworks like SimSiam, BYOL, and SimCLR, enabling efficient representation learning without labeled data. SimCLR, BYOL, and SimSiam, all employ the architecture inspired by Siamese networks, but they adapt the core principles in distinct ways to suit their specific self-supervised learning (SSL) objectives. Before learning about the Siamese Networks, first have a look at the similar architectures of various SSL frameworks.
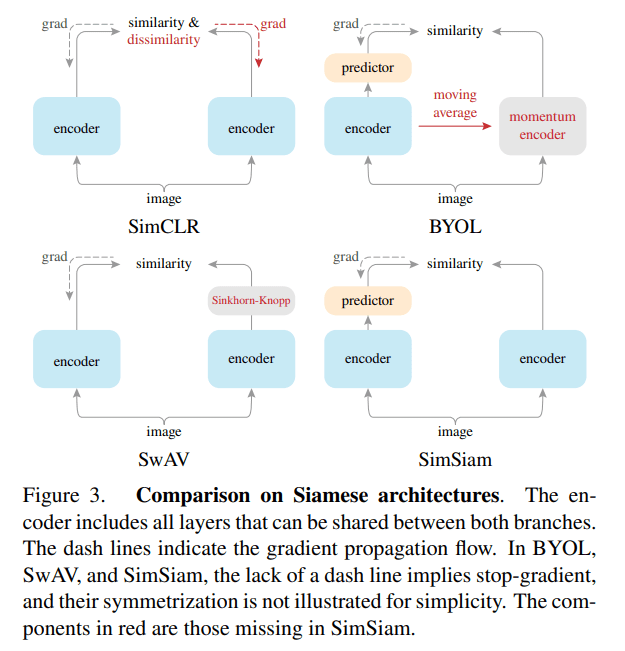
The above image clearly depicts the importance of Siamese architectures in modern Contrastive Learning frameworks such as SimCLR, BYOL, SimSiam, and many more.
Siamese Networks
Siamese Neural Networks serves as a critical component of SSL. They consist of two or more identical (weight-sharing) neural networks. These networks are applied to multiple inputs simultaneously to produce outputs that can be compared. Weight-sharing (unlike in BYOL or MoCo) ensures that both inputs are processed using the same parameters, making the network efficient for learning representations.
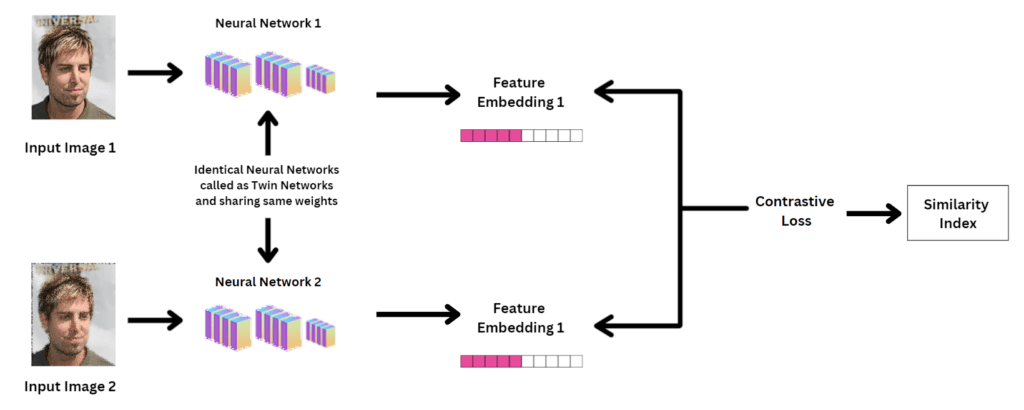
Siamese architecture plays a major role in achieving invariance (the ability of a model to produce the same outputs when observing different variations of the same concept or image). Drawing parallels with convolutional neural networks (CNNs), where weight-sharing in CNNs facilitates translation invariance, Siamese Networks, through the weight-sharing mechanism, manages the augmentation-based invariance enabling the model to maintain robustness across diverse augmented views of the same input.
Output Collapse
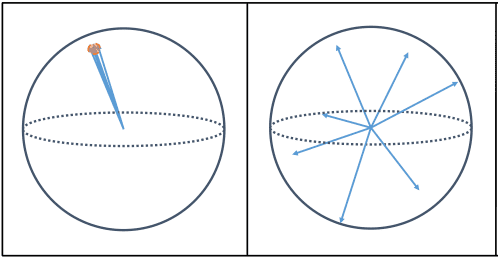
In representation learning, output collapse (the network producing identical outputs for all inputs, as can be seen in the left part of the above image, where the model maps all inputs to the same feature vector) is a big risk. Experiments show that collapsing solutions exist for SimSiam’s loss and structure, but a stop-gradient operation is essential in preventing collapse. The authors even have proof of concepts to verify it.
Apart from using the Stop-gradient operation, there are other multiple strategies also to prevent output collapse in Siamese networks, which include:
- Contrastive Learning – involves learning discriminative representations by bringing similar data points (positive pairs) closer in representation space while pushing dissimilar ones (negative pairs) farther apart. Example usage – SimCLR.
- Clustering-based methods – group similar data points into clusters and train the network to assign meaningful clusters for inputs. Example usage – DeepCluster
- SwAV (Swapped Assignment Between Views) – combines contrastive learning and clustering approaches. It avoids the collapse problem by performing online feature clustering while ensuring alignment between the clusters of different views (augmentations) of the same image.
Before we discuss SimSiam in more detail, let us first revise the general SSL workflow.
SSL General Workflow
- Generate Augmentations to create two augmented views – These augmentations are subject to different conditions, such as:
- Invariance: The network should produce similar embeddings regardless of the augmentation.
- Diversity: The learned representations should remain distinguishable across different images.
- Avoiding Collapse: Preventing the network from producing identical outputs for all inputs.
- Encode the augmented views into feature representations to learn a rich, high-level representation of the input data.
- Project Features to an Embedding Space to transform extracted features into a lower-dimensional embedding space where comparisons (e.g., similarity calculations) are more meaningful.
- To learn a mapping from the projected embeddings to a predicted space. The predictor helps the model align representations without collapsing into trivial solutions (e.g., predicting constant vectors).
- Compare Representations (Find Similarities) To align representations from different augmented views of the same input while keeping them distinct from other inputs.
- Prevent Collapse to avoid trivial solutions where the model produces identical embeddings for all inputs.
- Optimizing the Loss Function aligns the embeddings from different augmented views while preserving meaningful distinctions between different inputs.
SimSiam (Simple Siamese Networks)
SimSiam (Simple Siamese Networks) is an important follow-up concept in contrastive self-supervised learning, introduced by researchers at Facebook AI Research (FAIR). It removes the need for negative samples or momentum encoders, which were central in methods like SimCLR and BYOL. This simplicity makes SimSiam highly computationally efficient while retaining excellent performance.
As we are aware of SimCLR, BYOL, and SwAV, SimSiam can be thought of as BYOL without a Momentum Encoder. Unlike BYOL, like SimCLR and SwAV, SimSiam directly shares the weights between two of its branches. So, SimSiam can also be thought of as SimCLR without negative pairs and SwAV without Online Clustering. SimSiam is in fact related to each other by removing one of its core components.
Now, we’ll understand the SimSiam architecture in great detail along with the PyTorch implementation code of all of the components in the SimSiam architecture along with SimSiam’s pretraining and then fine-tuning its learned representations.
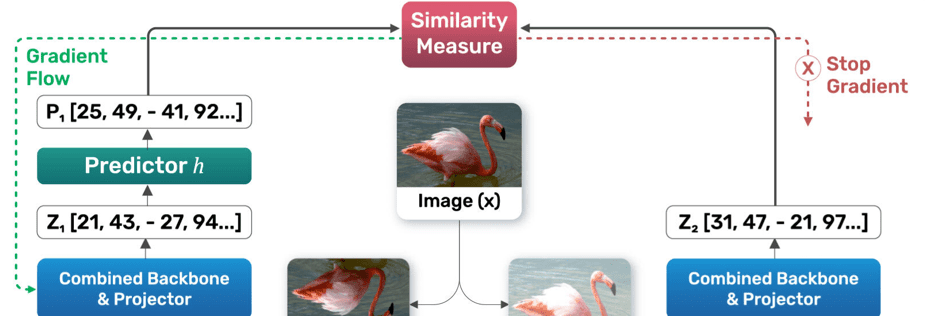
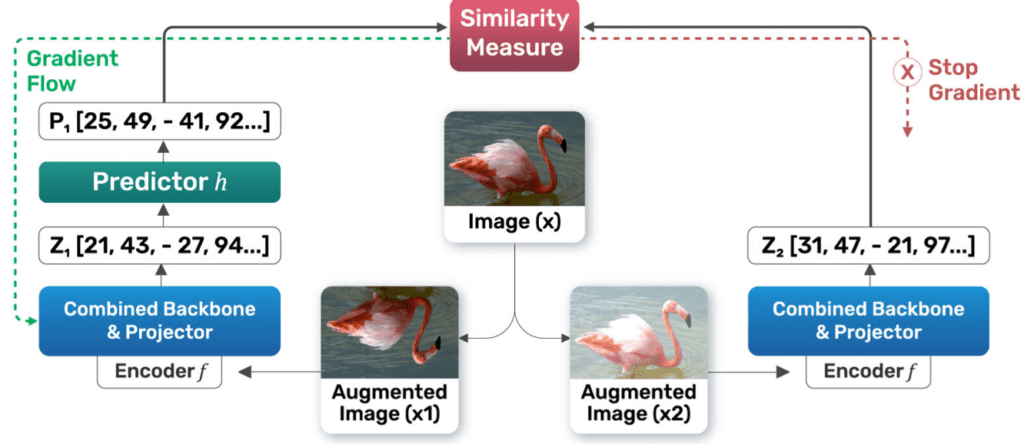
SimSiam Architecture
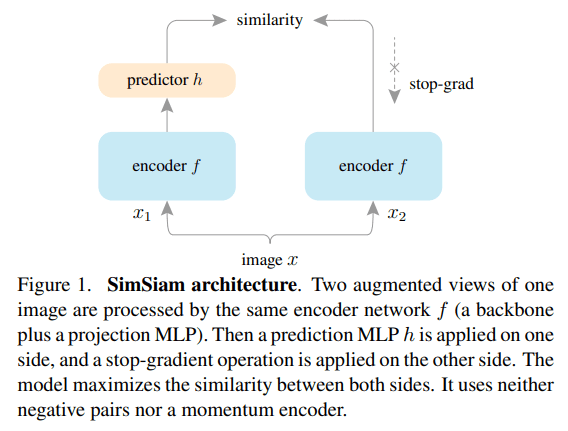
Overview of SimSiam’s Architecture
The architecture consists of:
- Two branches process two augmented views of the same input image (x), referred to as
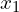 and
and 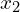 .
. - Each branch includes:
- An encoder network (
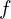 ): Composed of a backbone (e.g., ResNet) and a projection MLP.
): Composed of a backbone (e.g., ResNet) and a projection MLP. - A prediction MLP (
 ): Applied only to one branch (the “online” branch).
): Applied only to one branch (the “online” branch).
- An encoder network (
- A stop-gradient operation is applied to one branch to stabilize training and prevent trivial solutions (will be explained later in this article).
SimSiam’s Algorithm and Workflow

Workflow and its PyTorch implementation (Multi-GPU SimSiam’s Pretraining and Fine-Tuning code is attached although the parameters and experimental settings being initialized according to Single-GPU SimSiam’s Pretraining and then Fine-Tuning) according to the methodology configured in the official paper-
Input Augmentations:
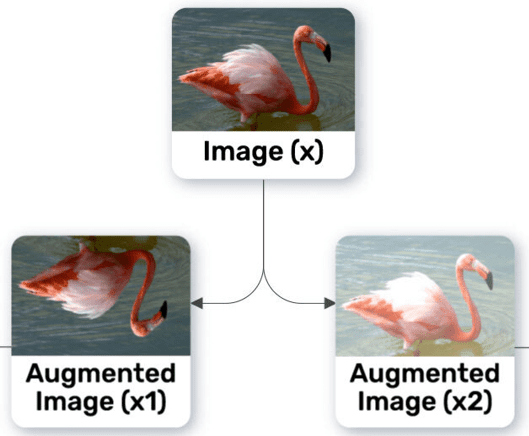
The input image (x) undergoes two independent augmentations to create ![]() and
and ![]() . These augmentations might include transformations like cropping, flipping, or color jittering.
. These augmentations might include transformations like cropping, flipping, or color jittering.
from PIL import ImageFilter
import random
class TwoCropsTransform:
"""
A transformation class to create two different random crops of the same image.
This is used to generate a query (q) and key (k) pair for contrastive learning.
"""
def __init__(self, base_transform):
# Initialize with a base transformation (e.g., augmentation pipeline).
self.base_transform = base_transform
def __call__(self, x):
# Apply the base transformation twice to produce two augmented views.
q = self.base_transform(x) # First crop (query)
k = self.base_transform(x) # Second crop (key)
return [q, k] # Return as a list of query and key
class GaussianBlur(object):
"""
Apply Gaussian blur as an augmentation.
This is inspired by SimCLR: https://arxiv.org/abs/2002.05709.
"""
def __init__(self, sigma=[.1, 2.]):
# Define the range for the standard deviation (sigma) of the Gaussian kernel.
self.sigma = sigma
def __call__(self, x):
# Randomly select a sigma value within the defined range.
sigma = random.uniform(self.sigma[0], self.sigma[1])
# Apply Gaussian blur with the selected radius to the input image.
x = x.filter(ImageFilter.GaussianBlur(radius=sigma))
return x
In the above code block, TwoCropsTransform Class generates two different random crops (augmentations) of the same input image. These crops are used as the query and key for self-supervised learning methods like SimSiam. GaussianBlur Class implements Gaussian blur as an image augmentation, inspired by its use in contrastive learning frameworks like SimCLR. GaussianBlur Class also implements sigma which defines the standard deviation for the Gaussian kernel.
Feature Extraction by Encoder (f):
- Both augmented views are processed by the shared encoder network (
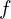 ), which extracts high-dimensional feature representations from each input:
), which extracts high-dimensional feature representations from each input:
- The encoder ensures the representations are invariant to the augmentations applied to the input.
'''
Reference:
[1] Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun
Deep Residual Learning for Image Recognition. arXiv:1512.03385
'''
class BasicBlock(nn.Module):
"""
Basic building block for ResNet.
Implements two convolutional layers with Batch Normalization and ReLU activation.
Includes a shortcut connection to handle dimensionality changes.
"""
expansion = 1 # Defines how the number of output channels expands
def __init__(self, in_planes, planes, stride=1):
super(BasicBlock, self).__init__()
# First convolutional layer
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(planes)
# Second convolutional layer
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
# Shortcut connection for matching dimensions if necessary
self.shortcut = nn.Sequential()
if stride != 1 or in_planes != self.expansion * planes:
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, self.expansion * planes, kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(self.expansion * planes)
)
def forward(self, x):
# Forward pass through convolutional layers and shortcut connection
out = F.relu(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
out += self.shortcut(x) # Add shortcut connection
out = F.relu(out) # Final ReLU activation
return out
class Bottleneck(nn.Module):
"""
Bottleneck block for ResNet.
Implements a three-layer structure to reduce computation while maintaining performance.
"""
expansion = 4 # Output channels are 4x the input channels
def __init__(self, in_planes, planes, stride=1):
super(Bottleneck, self).__init__()
# First convolutional layer (1x1)
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=1, bias=False)
self.bn1 = nn.BatchNorm2d(planes)
# Second convolutional layer (3x3)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
# Third convolutional layer (1x1)
self.conv3 = nn.Conv2d(planes, self.expansion * planes, kernel_size=1, bias=False)
self.bn3 = nn.BatchNorm2d(self.expansion * planes)
# Shortcut connection for matching dimensions if necessary
self.shortcut = nn.Sequential()
if stride != 1 or in_planes != self.expansion * planes:
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, self.expansion * planes, kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(self.expansion * planes)
)
def forward(self, x):
# Forward pass through the bottleneck layers and shortcut connection
out = F.relu(self.bn1(self.conv1(x)))
out = F.relu(self.bn2(self.conv2(out)))
out = self.bn3(self.conv3(out))
out += self.shortcut(x) # Add shortcut connection
out = F.relu(out) # Final ReLU activation
return out
class ResNet(nn.Module):
"""
ResNet model definition.
Builds the full network by stacking blocks and applying transformations.
"""
def __init__(self, block, num_blocks, low_dim=128):
super(ResNet, self).__init__()
self.in_planes = 64 # Initial number of input channels
# Initial convolutional layer
self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(64)
# Stacked layers using blocks
self.layer1 = self._make_layer(block, 64, num_blocks[0], stride=1)
self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)
self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)
self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2)
# Fully connected layer for output
self.fc = nn.Linear(512 * block.expansion, low_dim)
# self.l2norm = Normalize(2) # Optional normalization (commented out)
def _make_layer(self, block, planes, num_blocks, stride):
"""
Create a layer by stacking multiple blocks.
Handles downsampling when stride > 1.
"""
strides = [stride] + [1] * (num_blocks - 1) # First block handles downsampling
layers = []
for stride in strides:
layers.append(block(self.in_planes, planes, stride))
self.in_planes = planes * block.expansion # Update input channels for the next block
return nn.Sequential(*layers)
def forward(self, x):
# Forward pass through all layers of the network
out = F.relu(self.bn1(self.conv1(x))) # Initial layer
out = self.layer1(out) # Layer 1
out = self.layer2(out) # Layer 2
out = self.layer3(out) # Layer 3
out = self.layer4(out) # Layer 4
out = F.avg_pool2d(out, 4) # Global average pooling
out = out.view(out.size(0), -1) # Flatten
out = self.fc(out) # Fully connected layer
# out = self.l2norm(out) # Optional normalization (commented out)
return out
# ResNet variants with different depths
def ResNet18(low_dim=128):
return ResNet(BasicBlock, [2, 2, 2, 2], low_dim)
def ResNet34(low_dim=128):
return ResNet(BasicBlock, [3, 4, 6, 3], low_dim)
def ResNet50(low_dim=128):
return ResNet(Bottleneck, [3, 4, 6, 3], low_dim)
def ResNet101(low_dim=128):
return ResNet(Bottleneck, [3, 4, 23, 3], low_dim)
def ResNet152(low_dim=128):
return ResNet(Bottleneck, [3, 8, 36, 3], low_dim)
The BasicBlock Class out of the above code blocks implements the core building block for ResNet (used in ResNet-18 and ResNet-34) while the Bottleneck Class implements the bottleneck block (used in ResNet-50, ResNet-101, and ResNet-152). The classes also include self.shortcut implementation which in case input and output dimensions differ (due to stride or channels), uses a 1×1 convolution to match dimensions. It efficiently extracts hierarchical features from images using residual connections, enabling deep networks to avoid vanishing gradients and learn robust representations.
Projection MLP (Part of f):
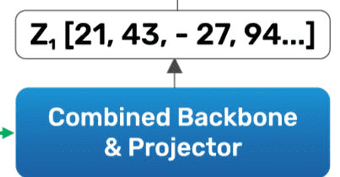
- The encoder network includes a projection MLP, which transforms the features into a lower-dimensional embedding space (
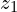 and
and 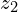 ) to improve representation learning.
) to improve representation learning. - The Projection MLP has a total of 3 layers. Batch Normalization has been applied to every Fully Connected FC layer including the Output FC layer. Output FC layer has no ReLU. The dimensionality of the hidden FC layer is 2048-d.
class projection_MLP(nn.Module):
"""
Multi-Layer Perceptron (MLP) for projection in SimSiam.
This module projects the backbone's output to a feature space for contrastive learning.
Args:
in_dim (int): Input feature dimension.
out_dim (int): Output feature dimension.
num_layers (int): Number of layers in the MLP (default: 2).
"""
def __init__(self, in_dim, out_dim, num_layers=2):
super().__init__()
hidden_dim = out_dim # Hidden layer dimension
self.num_layers = num_layers
# First layer: Fully connected + BatchNorm + ReLU
self.layer1 = nn.Sequential(
nn.Linear(in_dim, hidden_dim),
nn.BatchNorm1d(hidden_dim),
nn.ReLU(inplace=True)
)
# Second layer: Fully connected + BatchNorm + ReLU (optional)
self.layer2 = nn.Sequential(
nn.Linear(hidden_dim, hidden_dim),
nn.BatchNorm1d(hidden_dim),
nn.ReLU(inplace=True)
)
# Third layer: Fully connected + BatchNorm without learnable affine parameters
self.layer3 = nn.Sequential(
nn.Linear(hidden_dim, out_dim),
nn.BatchNorm1d(out_dim, affine=False) # See SimSiam paper (Page 5, Paragraph 2)
)
def forward(self, x):
"""
Forward pass through the projection MLP.
Args:
x (torch.Tensor): Input features.
Returns:
torch.Tensor: Projected features.
"""
if self.num_layers == 2:
x = self.layer1(x)
x = self.layer3(x)
elif self.num_layers == 3:
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
return x
In the above code block, the projection_MLP Class implements the projection head in SimSiam, which maps the output of the backbone encoder to a feature space for representation learning. We can infer from the projection_MLP implementation that for a 2-layered MLP, the flow is as follows – layer1 → layer3 while for a 3-layered MLP, the flow is layer1 → layer2 → layer3. The use of BatchNorm without affine parameters in the final layer ensures that the embeddings remain distributed on a unit hypersphere, as noted in the SimSiam paper. The projection MLP reduces the influence of biases in the backbone’s representations by mapping them into a more effective feature space for contrastive learning.
Prediction MLP (h):
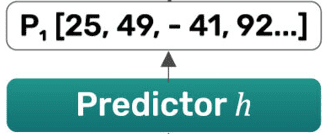
- The prediction MLP (
 ) is applied to the output of one branch (student or online branch) (e.g.,
) is applied to the output of one branch (student or online branch) (e.g., 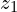 ) to produce
) to produce 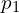 .
. - The other branch (
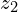 ) remains unchanged, with no prediction MLP applied.
) remains unchanged, with no prediction MLP applied. - The Prediction MLP has 2 layers. It has Batch Normalization applied to its hidden FC layers. Its Output FC layer does not have BN or ReLU. The dimension of
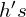 input and output (
input and output (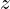 and
and 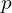 ) is d = 2048, and
) is d = 2048, and 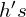 hidden layer’s dimension is 512, making
hidden layer’s dimension is 512, making  a bottleneck structure.
a bottleneck structure.
class prediction_MLP(nn.Module):
"""
MLP for prediction in SimSiam.
Maps the projected features to the prediction space.
Args:
in_dim (int): Input feature dimension (default: 2048).
"""
def __init__(self, in_dim=2048):
super().__init__()
out_dim = in_dim # Output dimension matches input dimension
hidden_dim = int(out_dim / 4) # Reduce feature dimension in the hidden layer
# First layer: Fully connected + BatchNorm + ReLU
self.layer1 = nn.Sequential(
nn.Linear(in_dim, hidden_dim),
nn.BatchNorm1d(hidden_dim),
nn.ReLU(inplace=True)
)
# Second layer: Fully connected (no activation)
self.layer2 = nn.Linear(hidden_dim, out_dim)
def forward(self, x):
"""
Forward pass through the prediction MLP.
Args:
x (torch.Tensor): Input features.
Returns:
torch.Tensor: Predicted features.
"""
x = self.layer1(x)
x = self.layer2(x)
return x
The prediction_MLP Class from the above-attached code block implements the prediction head in SimSiam, which maps the output of the projection MLP to a prediction space. This module is key to aligning embeddings between the two branches during self-supervised training. A fully connected linear layer reduces the feature dimensions to hidden_dim (set as in_dim/4). This design is critical to SimSiam’s success as it allows predictions (![]() and
and ![]() ) to align with their corresponding embeddings (
) to align with their corresponding embeddings (![]() and
and ![]() ).
).
Stop-Gradient Mechanism:
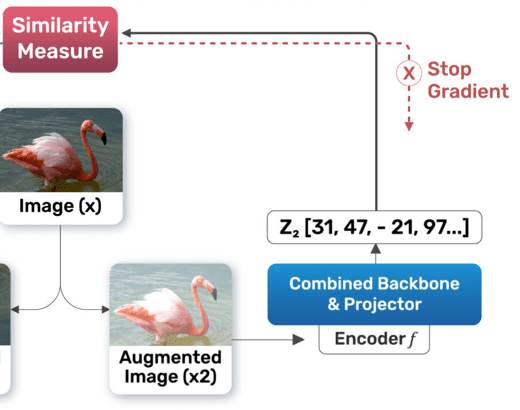
- The stop-gradient operation in SimSiam plays a crucial role in preventing representation collapse by ensuring that the target branch of the network remains fixed while training the online or student branch.
- For loss computation, the stop-gradient operation freezes the target branch output
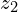 during loss computation which treats
during loss computation which treats 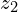 as a constant, so no gradients flow backward through
as a constant, so no gradients flow backward through 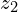 or the encoder
or the encoder 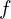 that produced it. Authors have implemented the same in the following way –
that produced it. Authors have implemented the same in the following way –
The above expression also works as the asymmetric variant of SimSiam’s loss function. - By stopping gradients through
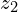 , the target branch becomes a fixed reference during the current optimization step. This ensures that the online branch (encoder
, the target branch becomes a fixed reference during the current optimization step. This ensures that the online branch (encoder 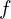 and Prediction MLP
and Prediction MLP  ) learns to align its output
) learns to align its output 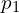 with the fixed
with the fixed 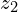 without modifying
without modifying 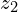 .
. - If gradients were allowed to flow through both
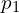 and
and 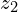 , the network might “shortcut” its learning process and it might collapse. By freezing
, the network might “shortcut” its learning process and it might collapse. By freezing 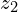 , only the online branch is updated, forcing it to align to a fixed target.
, only the online branch is updated, forcing it to align to a fixed target. - Combined with the prediction MLP, stop-gradient introduces enough asymmetry to avoid collapse without needing momentum encoders or negative pairs.
if self.ver == 'original':
# Detach z to stop gradient flow
z = z.detach()
#Loss Computation code
# has been omitted from here
elif self.ver == 'simplified':
# Detach z to stop gradient flow
z = z.detach()
The loss encourages similarity between predictions (![]() ) and projections (
) and projections (![]() ) without gradients flowing back through the projection branch (
) without gradients flowing back through the projection branch (![]() is detached).
is detached).
Similarity Maximization:
- The cosine similarity between
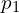 (from the prediction MLP) and
(from the prediction MLP) and 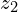 (from the second branch) is computed and maximized.
(from the second branch) is computed and maximized. - Similarly, the roles of
 and
and 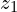 are reversed, and their similarity is also maximized.
are reversed, and their similarity is also maximized. - And this way, the original loss (asymmetric) implemented in the official paper is as follows –
- The objective ensures that the two branches produce similar embeddings for the two augmented views of the same image, encouraging the network to learn meaningful representations.
class SimSiamLoss(nn.Module):
"""
Implementation of the SimSiam loss function.
This loss is designed for self-supervised learning by comparing the similarity
between pairs of projections and predictions from two augmented views of the same image.
Reference:
SimSiam: Exploring Simple Siamese Representation Learning (https://arxiv.org/abs/2011.10566)
"""
def __init__(self, version='simplified'):
"""
Initialize the SimSiam loss module.
Args:
version (str): Specifies the version of the loss.
'original' uses the original dot-product-based formulation,
'simplified' uses cosine similarity (default).
"""
super().__init__()
self.ver = version
def asymmetric_loss(self, p, z):
"""
Compute the asymmetric loss between the prediction (p) and the projection (z).
This enforces similarity between the two while detaching the gradient from `z`.
Args:
p (torch.Tensor): Prediction vector.
z (torch.Tensor): Projection vector.
Returns:
torch.Tensor: Computed loss.
"""
if self.ver == 'original':
# Detach z to stop gradient flow
z = z.detach()
# Normalize vectors
p = nn.functional.normalize(p, dim=1)
z = nn.functional.normalize(z, dim=1)
# Original formulation: negative dot product
return -(p * z).sum(dim=1).mean()
elif self.ver == 'simplified':
# Detach z to stop gradient flow
z = z.detach()
# Simplified formulation: negative cosine similarity
return -nn.functional.cosine_similarity(p, z, dim=-1).mean()
def forward(self, z1, z2, p1, p2):
"""
Compute the SimSiam loss for two pairs of projections and predictions.
Args:
z1 (torch.Tensor): Projection vector from the first augmented view.
z2 (torch.Tensor): Projection vector from the second augmented view.
p1 (torch.Tensor): Prediction vector corresponding to z1.
p2 (torch.Tensor): Prediction vector corresponding to z2.
Returns:
torch.Tensor: Averaged SimSiam loss.
"""
# Compute the loss for each pair (p1, z2) and (p2, z1)
loss1 = self.asymmetric_loss(p1, z2)
loss2 = self.asymmetric_loss(p2, z1)
# Average the two losses
return 0.5 * loss1 + 0.5 * loss2
As we can infer from the above code block about the implementation of SimSiam Loss, SimSiamLoss Class implements the loss function for SimSiam. asymmetric_loss Method computes the similarity-based loss for one prediction-projection pair while ensuring that no gradients flow through the projection vector (![]() ). The original version uses the negative dot product between
). The original version uses the negative dot product between ![]() and
and ![]() while the simplified version uses negative cosine similarity, which is computationally efficient and aligns with the unit-norm constraint.
while the simplified version uses negative cosine similarity, which is computationally efficient and aligns with the unit-norm constraint.
SimSiam Pipeline Implementation
The definition of the SimSiam model is as follows –
class SimSiam(nn.Module):
"""
SimSiam network implementation.
Combines a backbone, a projection MLP, and a prediction MLP for self-supervised learning.
Args:
args (Namespace): Configuration arguments for the model.
"""
def __init__(self, args):
super(SimSiam, self).__init__()
# Initialize the backbone (e.g., ResNet variants)
self.backbone = SimSiam.get_backbone(args.arch)
out_dim = self.backbone.fc.weight.shape[1] # Feature dimension from the backbone
self.backbone.fc = nn.Identity() # Remove the fully connected layer from the backbone
# Initialize the projection MLP
self.projector = projection_MLP(out_dim, args.feat_dim, args.num_proj_layers)
# Combine backbone and projector into a single encoder
self.encoder = nn.Sequential(
self.backbone,
self.projector
)
# Initialize the prediction MLP
self.predictor = prediction_MLP(args.feat_dim)
@staticmethod
def get_backbone(backbone_name):
"""
Retrieve the backbone model based on the specified architecture.
Args:
backbone_name (str): Name of the backbone architecture.
Returns:
nn.Module: Backbone model instance.
"""
return {
'resnet18': ResNet18(),
'resnet34': ResNet34(),
'resnet50': ResNet50(),
'resnet101': ResNet101(),
'resnet152': ResNet152()
}[backbone_name]
def forward(self, im_aug1, im_aug2):
"""
Forward pass through the SimSiam model.
Args:
im_aug1 (torch.Tensor): Augmented view 1 of the input image batch.
im_aug2 (torch.Tensor): Augmented view 2 of the input image batch.
Returns:
dict: Output projections and predictions for both views.
Keys: 'z1', 'z2', 'p1', 'p2'
"""
# Pass the first augmented view through the encoder
z1 = self.encoder(im_aug1)
# Pass the second augmented view through the encoder
z2 = self.encoder(im_aug2)
# Predict features for both views
p1 = self.predictor(z1)
p2 = self.predictor(z2)
# Return projections and predictions
return {'z1': z1, 'z2': z2, 'p1': p1, 'p2': p2}
The SimSiam Class implements the complete SimSiam architecture, combining a backbone encoder, a projection MLP, and a prediction MLP for self-supervised learning. While initialization, we can see that the Fully Connected (FC) layer from the backbone has been removed by replacing it with nn.Identity (since SimSiam adds its projection MLP).
Now, we can move to pretraining SimSiam. All of the experimental settings have been grouped into a single, editable block, simplifying experimentation. Therefore, it is easy to modify parameters like batch size, learning rate, or architecture for different experiments. It will also ensure that the code runs seamlessly in notebook environments without parsing errors.
Experimental Settings for Pretraining SimSiam
import argparse
import sys
# Adjust `sys.argv` for compatibility with Jupyter Notebook or IPython environments.
if 'ipykernel_launcher' in sys.argv[0]:
sys.argv = [sys.argv[0]] # Reset `sys.argv` to prevent parsing issues.
# Define configuration parameters for the SimSiam experiment using argparse.Namespace.
args = argparse.Namespace(
data_root='./data', # Path to the root directory containing dataset.
exp_dir='./experiments', # Directory for saving experimental results (e.g., checkpoints, logs).
trial='1', # Identifier for the experiment trial.
img_dim=32, # Dimension of the input images (e.g., 32x32 for CIFAR-10).
arch='resnet18', # Backbone architecture to use (e.g., ResNet18).
feat_dim=2048, # Dimensionality of the projected features.
num_proj_layers=2, # Number of layers in the projection MLP.
batch_size=512, # Batch size for training and validation.
num_workers=4, # Number of data loading workers.
epochs=800, # Number of training epochs.
gpu=0, # GPU index to use for training (e.g., 0 for the first GPU).
loss_version='simplified', # Version of the loss function ('simplified' or 'original').
print_freq=10, # Frequency (in batches) to print training progress.
eval_freq=5, # Frequency (in epochs) to perform KNN evaluation.
save_freq=50, # Frequency (in epochs) to save model checkpoints.
resume=None, # Path to a checkpoint file to resume training, if any.
learning_rate=0.06, # Initial learning rate for the optimizer.
weight_decay=5e-4, # Weight decay for regularization.
momentum=0.9 # Momentum for the SGD optimizer.
)
# Print the parsed arguments for verification and debugging
print("Parsed Arguments:", args)
SimSiam’s Pretraining Implementation in PyTorch
import time
import math
from os import path, makedirs
import torch
from torch import optim
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
from torch.backends import cudnn
from torchvision import datasets
from torchvision import transforms
def main():
"""
Main function to set up training and validation for SimSiam.
Handles directory creation, data preparation, model setup, training loop, and checkpointing.
"""
# Create experiment directory if it doesn't exist
if not path.exists(args.exp_dir):
makedirs(args.exp_dir)
# Setup trial-specific directory and logger for TensorBoard
trial_dir = path.join(args.exp_dir, args.trial)
logger = SummaryWriter(trial_dir)
print(vars(args)) # Print experiment configuration
# Define data augmentation for training
train_transforms = transforms.Compose([
transforms.RandomResizedCrop(args.img_dim, scale=(0.2, 1.)),
transforms.RandomHorizontalFlip(),
transforms.RandomApply([
transforms.ColorJitter(0.4, 0.4, 0.4, 0.1) # Random brightness, contrast, saturation, hue
], p=0.8),
transforms.RandomGrayscale(p=0.2),
transforms.ToTensor(),
transforms.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010)) # MNIST mean and std
])
# Load CIFAR-10 training dataset with TwoCropsTransform for SimSiam
train_set = datasets.CIFAR10(root=args.data_root,
train=True,
download=True,
transform=TwoCropsTransform(train_transforms))
train_loader = DataLoader(dataset=train_set,
batch_size=args.batch_size,
shuffle=True,
num_workers=args.num_workers,
pin_memory=True,
drop_last=True)
# Initialize SimSiam model
model = SimSiam(args)
# Define SGD optimizer with momentum and weight decay
optimizer = optim.SGD(model.parameters(),
lr=args.learning_rate,
momentum=args.momentum,
weight_decay=args.weight_decay)
# Initialize loss function (original or simplified version)
criterion = SimSiamLoss(args.loss_version)
# Move model and loss to GPU if available
if args.gpu is not None:
torch.cuda.set_device(args.gpu)
model = model.cuda(args.gpu)
criterion = criterion.cuda(args.gpu)
cudnn.benchmark = True # Enable auto-tuning for faster training
# Resume from a checkpoint if provided
start_epoch = 1
if args.resume is not None:
if path.isfile(args.resume):
start_epoch, model, optimizer = load_checkpoint(model, optimizer, args.resume)
print("Loaded checkpoint '{}' (epoch {})".format(args.resume, start_epoch))
else:
print("No checkpoint found at '{}'".format(args.resume))
# Training and validation loop
best_acc = 0.0
validation = KNNValidation(args, model.encoder) # Initialize KNN validation
for epoch in range(start_epoch, args.epochs + 1):
adjust_learning_rate(optimizer, epoch, args) # Update learning rate
print("Training...")
# Train for one epoch
train_loss = train(train_loader, model, criterion, optimizer, epoch, args)
logger.add_scalar('Loss/train', train_loss, epoch) # Log training loss
# Perform KNN validation periodically
if epoch % args.eval_freq == 0:
print("Validating...")
val_top1_acc = validation.eval() # Evaluate KNN accuracy
print('Top1: {}'.format(val_top1_acc))
# Save the best model checkpoint
if val_top1_acc > best_acc:
best_acc = val_top1_acc
save_checkpoint(epoch, model, optimizer, best_acc,
path.join(trial_dir, '{}_best.pth'.format(args.trial)),
'Saving the best model!')
logger.add_scalar('Acc/val_top1', val_top1_acc, epoch) # Log validation accuracy
# Save model periodically
if epoch % args.save_freq == 0:
save_checkpoint(epoch, model, optimizer, val_top1_acc,
path.join(trial_dir, 'ckpt_epoch_{}_{}.pth'.format(epoch, args.trial)),
'Saving...')
print('Best accuracy:', best_acc)
# Save the final model checkpoint
save_checkpoint(epoch, model, optimizer, val_top1_acc,
path.join(trial_dir, '{}_last.pth'.format(args.trial)),
'Saving the model at the last epoch.')
Implementation of the main() function which handles directory creation, data preparation, model setup, training loop, validation for SimSiam, and checkpointing.
def train(train_loader, model, criterion, optimizer, epoch, args):
"""
Train the SimSiam model for one epoch.
Args:
train_loader (DataLoader): DataLoader for training data.
model (nn.Module): SimSiam model.
criterion (nn.Module): Loss function (e.g., SimSiamLoss).
optimizer (Optimizer): Optimizer (e.g., SGD).
epoch (int): Current epoch number.
args (Namespace): Experiment arguments.
Returns:
float: Average training loss for the epoch.
"""
batch_time = AverageMeter('Time', ':6.3f') # Measure batch processing time
losses = AverageMeter('Loss', ':.4e') # Track average loss
progress = ProgressMeter(
len(train_loader),
[batch_time, losses],
prefix="Epoch: [{}]".format(epoch))
model.train() # Set model to training mode
end = time.time()
for i, (images, _) in enumerate(train_loader):
if args.gpu is not None:
images[0] = images[0].cuda(args.gpu, non_blocking=True)
images[1] = images[1].cuda(args.gpu, non_blocking=True)
# Forward pass through the model
outs = model(im_aug1=images[0], im_aug2=images[1])
loss = criterion(outs['z1'], outs['z2'], outs['p1'], outs['p2']) # Compute SimSiam loss
# Backpropagation and optimization
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Update loss and batch time
losses.update(loss.item(), images[0].size(0))
batch_time.update(time.time() - end)
end = time.time()
if i % args.print_freq == 0: # Display progress periodically
progress.display(i)
return losses.avg # Return average loss
Implementation of the train() function which is supposed to train the SimSiam model for one epoch.
def adjust_learning_rate(optimizer, epoch, args):
"""
Adjust the learning rate using a cosine annealing schedule.
Args:
optimizer (Optimizer): Optimizer to update.
epoch (int): Current epoch number.
args (Namespace): Experiment arguments.
"""
lr = args.learning_rate * 0.5 * (1. + math.cos(math.pi * epoch / args.epochs))
for param_group in optimizer.param_groups:
param_group['lr'] = lr
adjust_learning_rate() function to implement the Cosine Annealing Schedule to adjust the learning rates during pretraining SimSiam.
class AverageMeter(object):
"""
Helper class to compute and store the average and current value of metrics.
"""
def __init__(self, name, fmt=':f'):
self.name = name
self.fmt = fmt
self.val = 0
self.avg = 0
self.sum = 0
self.count = 0
self.reset()
def reset(self):
self.val = 0
self.avg = 0
self.sum = 0
self.count = 0
def update(self, val, n=1):
self.val = val
self.sum += val * n
self.count += n
self.avg = self.sum / self.count
def __str__(self):
fmtstr = '{name} {val' + self.fmt + '} ({avg' + self.fmt + '})'
return fmtstr.format(**self.__dict__)
Helper class to compute and store the average and current value of metrics.
class ProgressMeter(object):
"""
Helper class to display progress during training or validation.
"""
def __init__(self, num_batches, meters, prefix=""):
self.batch_fmtstr = self._get_batch_fmtstr(num_batches)
self.meters = meters
self.prefix = prefix
def display(self, batch):
entries = [self.prefix + self.batch_fmtstr.format(batch)]
entries += [str(meter) for meter in self.meters]
print('\t'.join(entries))
def _get_batch_fmtstr(self, num_batches):
num_digits = len(str(num_batches // 1))
fmt = '{:' + str(num_digits) + 'd}'
return '[' + fmt + '/' + fmt.format(num_batches) + ']'
Helper class to display progress during training or validation.
def save_checkpoint(epoch, model, optimizer, acc, filename, msg):
"""
Save model checkpoint.
Args:
epoch (int): Current epoch number.
model (nn.Module): Model to save.
optimizer (Optimizer): Optimizer to save.
acc (float): Accuracy value to save.
filename (str): Path to save the checkpoint file.
msg (str): Message to display after saving.
"""
state = {
'epoch': epoch,
'arch': args.arch,
'state_dict': model.state_dict(),
'optimizer': optimizer.state_dict(),
'top1_acc': acc
}
torch.save(state, filename)
print(msg)
Helper function for saving checkpoints.
def load_checkpoint(model, optimizer, filename):
"""
Load model checkpoint.
Args:
model (nn.Module): Model to load checkpoint into.
optimizer (Optimizer): Optimizer to load checkpoint into.
filename (str): Path to the checkpoint file.
Returns:
tuple: (start_epoch, model, optimizer)
"""
checkpoint = torch.load(filename, map_location='cuda:0')
start_epoch = checkpoint['epoch']
model.load_state_dict(checkpoint['state_dict'])
optimizer.load_state_dict(checkpoint['optimizer'])
return start_epoch, model, optimizer
if __name__ == '__main__':
main()
Helper function for loading checkpoints and the main() function to trigger SimSiam’s pretraining.
The above code blocks collectively outline the SimSiam framework’s training pipeline, from data preparation to training and validation. It includes helper functions for logging, saving/loading checkpoints, and managing training dynamics. If args.resume is provided, load the model and optimizer state to resume training from the last checkpoint. The training loop performs KNN-based validation periodically to evaluate the learned representations. adjust_learning_rate() implements a cosine annealing schedule to adjust the learning rate during training.
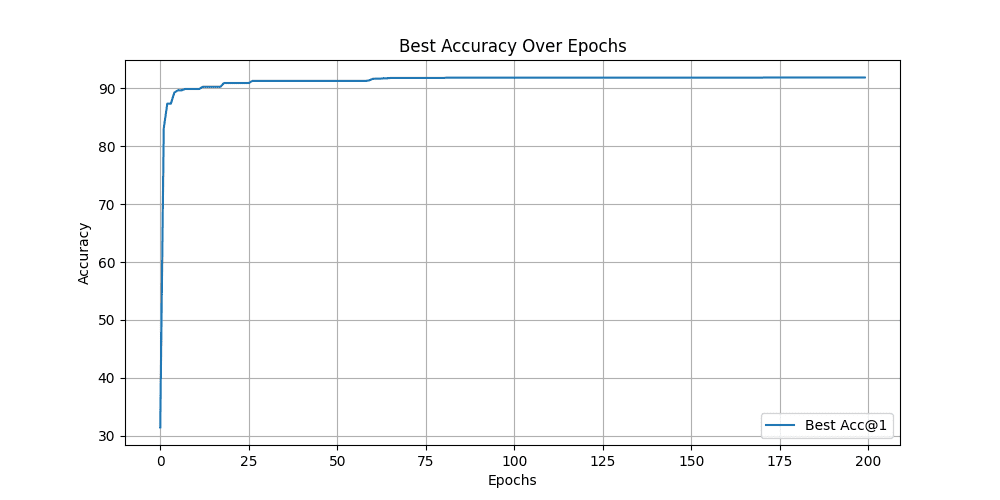
Implementation code for KNN-validation and fine-tuning of SimSiam’s learned representations downstreamed for classification task on the CIFAR-10 dataset has also been made available all in a single Google Colab notebook which can directly be downloaded. SimSiam’s pretrained weights over 800 epochs will also be downloaded along with the the Colab notebook. So we can even directly move over to analyze the effectiveness of SimSiam’s learned pretrained weights while fine-tuning.
The Validation Accuracy plot after fine-tuning SimSiam’s learned representations over 200 epochs for the classification task on the CIFAR-10 dataset is represented below –
Key Features of the SimSiam Framework’s Algorithm
- No Negative Pairs:
- Unlike contrastive methods like SimCLR, SimSiam does not use negative pairs, simplifying the training process and removing the need for large batch sizes.
- No Momentum Encoder:
- Unlike BYOL, SimSiam does not require a teacher network or momentum encoder. Instead, it relies on the stop-gradient mechanism to provide stability during training.
- Asymmetric Design:
- The asymmetry arises from applying the prediction MLP to one branch and the stop-gradient to the other. This asymmetry is critical to prevent collapse (i.e., trivial solutions where all outputs are identical).
The goal of SimSiam is to maximize the similarity between the embeddings of the two augmented views while avoiding collapse. By leveraging the stop-gradient mechanism and the asymmetry in the branches, SimSiam achieves this without requiring negatives or a teacher, making it a simpler yet effective SSL framework.
Investigating SimSiam’s Non-Collapsing Dynamics
- Stop-Gradient – The stop-gradient mechanism in SimSiam is pivotal for avoiding collapsing solutions by maintaining stable and diverse embeddings. This is empirically validated through ℓ2-normalized output’s standard deviation (std) and kNN accuracy. The standard deviation (std) of ℓ2-normalized outputs (z/||z||2) is used to diagnose collapse. When outputs collapse, their std approaches zero (indicating constant vectors). However, with stop-gradient, the std remains close to 1/sqrt(d) where d refers to the dimensionality of the embedding vector, suggesting embeddings are scattered on a unit hypersphere, avoiding collapse. With stop-gradient, the kNN accuracy steadily improves, indicating effective representation learning. Removing the stop-gradient causes accuracy to plummet to 0.1%. Without this mechanism, SimSiam degenerates to constant outputs. The introduction of stop-gradient implies that there should be another optimization problem that is being solved underlying which has been hypothesized in the later section of this article.
- Predictor
The model doesn’t work after removing the Predictor (h). Both symmetric and asymmetric variants (based on the symmetric and asymmetric loss used) of the network fail after removing h. And even simply initializing h randomly does not suffice, as the model still fails to converge. This result highlights that h must actively adapt during training rather than serve as a fixed component.
Another notable insight is that training h with a constant learning rate (without decay) yields better results compared to applying a learning rate decay. The hypothesis is that h should dynamically adapt to the evolving representations during training.
- Batch-size – SimSiam achieves consistent performance over varying batch sizes. Smaller batch sizes like 64 or 128 result in only a minimal accuracy drop of 0.8% to 2.0%, while batch sizes ranging from 256 to 2048 deliver similar results with random-level variations. This highlights the flexibility and robustness of SimSiam, even with smaller batches, unlike methods like SimCLR and SwAV, which also use Siamese architectures, and exhibit a dependency on larger batch sizes (e.g., 4096) to achieve optimal performance. While specialized optimizers such as LARS are typically recommended for such scenarios, the study reveals that they are not essential for preventing collapsing solutions in SimSiam.
- Batch-Normalization – The removal of all BN layers from the MLP heads results in a significant drop in accuracy to 34.6%, primarily attributed to optimization difficulties rather than collapsing behavior. Introducing BN in the hidden layers raises accuracy to 67.4%, showcasing its efficacy in stabilizing optimization. Further refinement, by adding BN to the output of the projection MLP f, boosts accuracy slightly further to 68.1%. BN includes learnable affine transformations and disabling that improves accuracy from 68.1% to 68.2%. BN to Prediction MLP doesn’t work well. This instability is not related to the collapse but rather to poor optimization dynamics.
- Similarity Function – The study reveals that replacing cosine similarity with cross-entropy similarity results in a slightly reduced accuracy (63.2% vs. 68.1%) but maintains non-collapsing solutions. This confirms that the collapsing prevention behavior of SimSiam is not solely dependent on the use of cosine similarity. Instead, it demonstrates that the architectural design and mechanisms, such as stop-gradient, are pivotal in achieving stability. The use of cross-entropy similarity also establishes a conceptual connection to SwAV where hyperparameters and architectures were not specifically tuned for cross-entropy similarity, its success in preventing collapse underscores the flexibility of SimSiam’s framework in adapting to different similarity measures.
- Symmetrization – Experimental results show that SimSiam’s ability to avoid collapsing solutions is not dependent on symmetrization. The asymmetric variant (Equation 3), which computes the loss in only one direction, achieves reasonable performance, with an accuracy of 64.8% compared to 68.1% for the symmetric loss. Symmetrization provides a slight boost in accuracy but is not integral to preventing collapse. The findings underscore that while symmetrization enhances performance, its role is more aligned with accuracy improvement rather than stability in representation learning.
Understanding SimSiam’s Implicit Optimization Dynamics
- Authors have hypothesized that SimSiam is an implementation of an Expectation-Maximization (EM) like approach that operates with two sets of variables, solving two subproblems iteratively. The approach is believed to iteratively learn meaningful representations by minimizing the discrepancy between projections and predictions of augmented views, effectively “expecting” consistent representations and “maximizing” alignment without relying on negative samples or explicit teachers. The loss function used –
The loss function, L(θ,η), combines the network parameters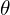 and the auxiliary variables
and the auxiliary variables 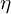 (represents the image’s embedding across augmentations) which is analogous to k-means clustering, where θ represents the encoder’s learnable parameters and η corresponds to cluster assignments. Now, the objective is to jointly optimize the loss function L(θ,η) by –
(represents the image’s embedding across augmentations) which is analogous to k-means clustering, where θ represents the encoder’s learnable parameters and η corresponds to cluster assignments. Now, the objective is to jointly optimize the loss function L(θ,η) by –
To solve, the optimization alternates between two sub-problems:
Authors believe that –
During optimization, the stop-gradient mechanism emerges naturally when solving for while treating
while treating  as constant. This prevents gradient flow through
as constant. This prevents gradient flow through  , simplifying the optimization.
, simplifying the optimization.
While solving for , the optimal value of
, the optimal value of 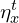 aligns with the mean of all augmented representations of x, ensuring consistency.
aligns with the mean of all augmented representations of x, ensuring consistency.
- When authors introduced Predictor
 in the above EM approach, they could hypothesize that Predictor
in the above EM approach, they could hypothesize that Predictor  aligns the output of one augmented view with the expected representation of another. This enables the model to approximate ET (Expectation introduced in the EM approach) without explicitly computing it.
aligns the output of one augmented view with the expected representation of another. This enables the model to approximate ET (Expectation introduced in the EM approach) without explicitly computing it.
- While symmetrization is not necessary for SimSiam’s effectiveness, it improves empirical accuracy, likely due to enhanced empirical expectation precision.
- We can conclude that the stop-gradient operation and the design of h naturally lead to its success without requiring negative samples or momentum encoders, unlike other contrastive learning methods.
Extended Insights
- Multi-step Alteration – SimSiam’s algorithm alternates between the above EM’s optimization’s two sub-problems with an interval of one SGD update.
- The authors pointed out that SimSiam and its variants’ non-collapsing behavior remains an empirical observation field.
- Prediction MLP’s hidden layer dimension being 1/4th of the output layer’s dimension acts as a more robust bottleneck structure.
Conclusion
SimSiam marks a breakthrough in self-supervised learning (SSL) with its modified design, eliminating the need for negative samples, momentum encoders, or teacher-student frameworks. By employing a dual-branch Siamese network with a stop-gradient mechanism and a predictor MLP, SimSiam ensures stable training and non-collapsing solutions. Unlike SimCLR and BYOL, it performs effectively across varying batch sizes and optimizers, without relying on specialized configurations.
Its use of cosine similarity, coupled with asymmetrized loss, simplifies representation learning while remaining robust to alternative similarity metrics like cross-entropy. Empirical studies further validate the importance of design elements such as batch normalization and the predictor MLP. SimSiam redefines SSL by offering a simple yet powerful framework, setting a strong foundation for future advancements in the field.
References
- SimSiam (Simple Siamese) Neural Networks
- Siamese Networks
- Dimensional Collapse in Contrastive Self-Supervised Learning
- Official SimSiam’s PyTorch Implementation







100K+ Learners
Join Free OpenCV Bootcamp3 Hours of Learning