3D Gaussian splatting (3DGS) has recently gained recognition as a groundbreaking approach in radiance fields and computer graphics. It stands out as a jack of all trades, addressing challenges that NeRF was originally designed to tackle, such as high-fidelity novel view synthesis (NVS), accurate 3D reconstruction, fast rendering, and relatively quicker training.

There are several challenges with Gaussian splatting, such as achieving photo-realism, managing high storage requirements, and floaters being one of them. Floaters are the Gaussian clouds that often arise from exposure or color inconsistencies in input images or may result from outliers generated during Structure-from-Motion (SfM) processes. Furthermore, Gaussian Splatting, in its true sense, is more about 3D reconstruction than novel view synthesis. It can only produce novel views for parts of the scene that are well-covered in the input image sequence.
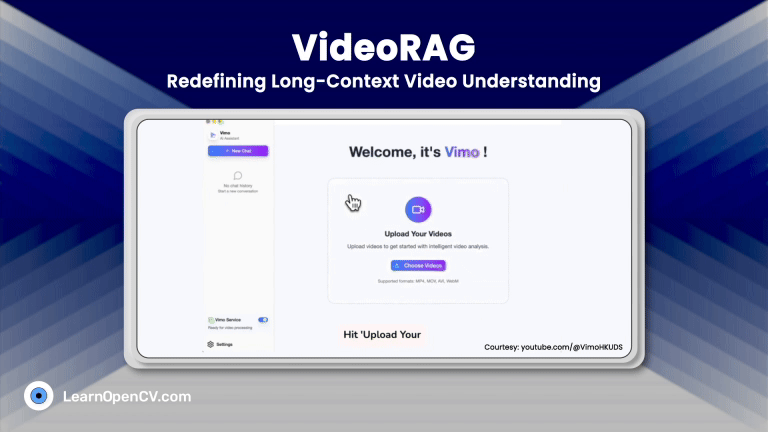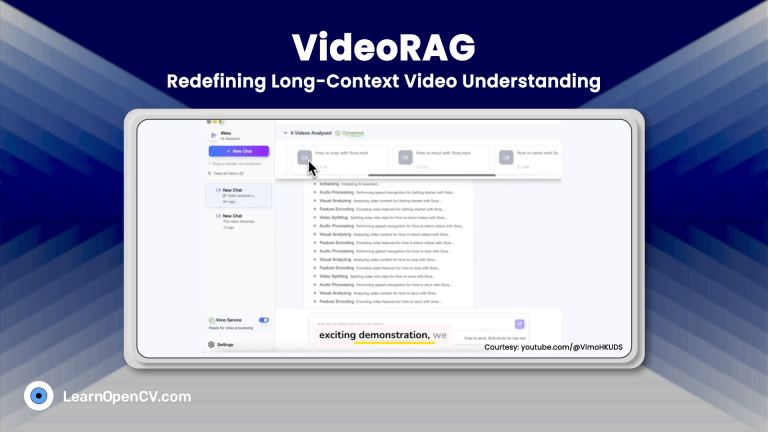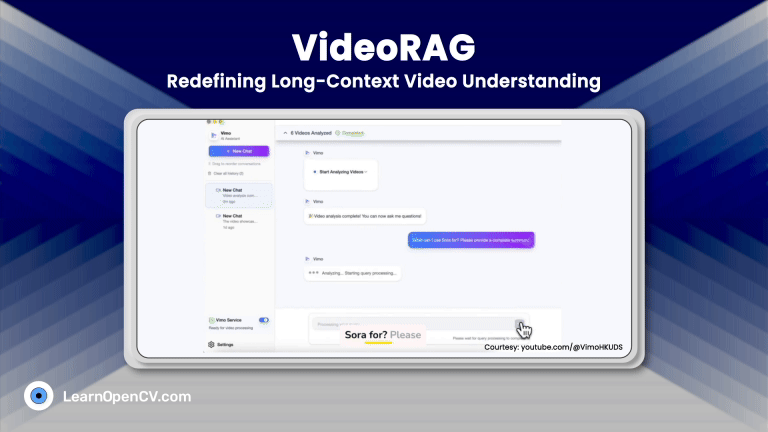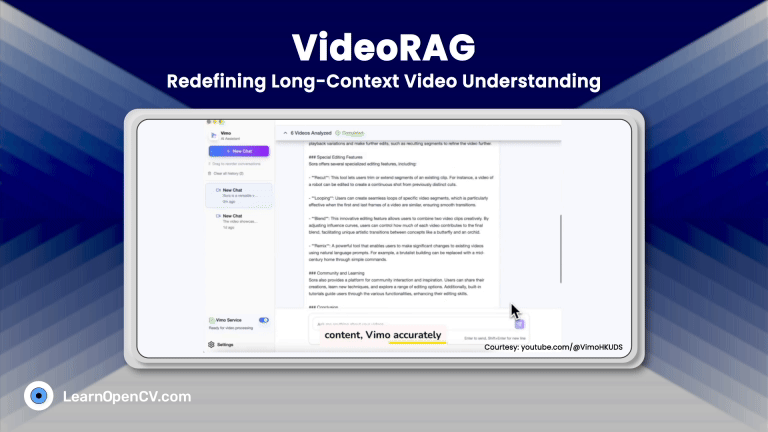
In this series of articles on 3D computer vision and graphics, we have so far covered NeRF and Gaussian Splatting in depth, including how to train them. In this article, we focus on an application of 3D Gaussian Splatting: object insertion in Gaussian Splatting. Additionally, we will provide a detailed explanation of the paper “3D Gaussian Splatting as Monte Carlo Markov Chain” (3DGS as MCMC).
If you’re familiar with the 3D Gaussian Splatting paper or have read the earlier “Introduction to 3D Gaussian Splatting” article, it will help you better understand the rest of this article.
- Introduction to 3DGS MCMC
- Implement Object Insertion in Gaussian Splatting
- Key Takeaways
- Conclusion
- References
Introduction to 3DGS MCMC
The premise of the 3DGS as MCMC paper is as follows:
- Probabilistic Notion to ADC: Although Adaptive Density Control (ADC) is an effective strategy for densification and pruning, it lacks a solid mathematical foundation. MCMC introduces a probabilistic framework to address this gap.
- Convergence and Exploration: Instead of relying solely on an optimization-based approach, the MCMC paper combines optimization with exploration, allowing for the identification of multiple optimal solutions to the problem.
- Move Dead to Live: ADC heuristics are replaced with state transitions implemented through relocation of the dead Gaussians.
- Introducing Regularization: The paper also introduces two types of regularization to the loss function: scale regularization and opacity regularization.

Let’s understand the above contributions in detail. We will dive deep into the mathematics of 3DGS as MCMC paper, and understand everything step by step. If you are only interested in learning how to insert objects into Gaussian Splatting, feel free to skip to that section of the article.
What is MCMC?
MCMC sampling, is a well known approximation algorithm, in Machine Learning, widely used in probabilistic modeling. Full form of MCMC is Monte Carlo Markov Chain. Notice, Monte Carlo and Markov Chain are two different algorithms. Let’s understand how are they working together.
Sometimes there are some sums of integrals that are very hard to compute directly because of many reasons such as complexity of the space, high dimensionality etc. In those scenarios, we approximating it – either by employing a sampling method, such as MCMC, or by using a parameterized distribution, as done in Variational Inference.
For instance, in Bayesian statistics, calculating the posterior distribution requires evaluating an integral over all possible values of the model parameters, weighted by the prior and the likelihood of the observed data. This integral can quickly become intractable as the number of parameters increases or the likelihood function becomes complex.
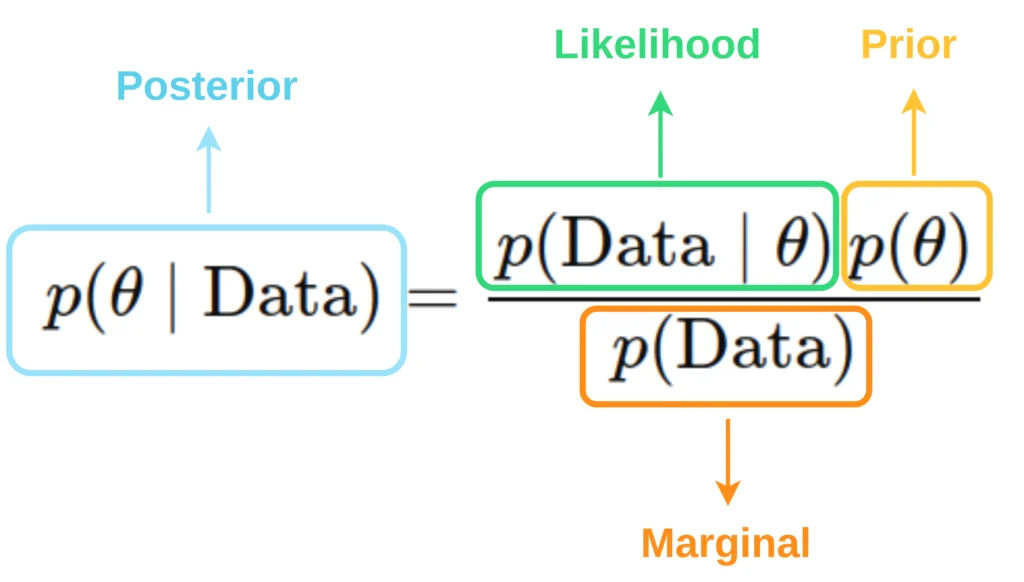
From the above image it might be clear what is prior, posterior and likelihood mathematically. We can understand it better with an example.
Imagine you’re guessing someone’s height(![]() ) based on their shoe size(
) based on their shoe size(![]() ).
).
- Prior: The prior distribution, denoted as
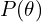 , represents any assumptions you have before observing the actual data. For instance, you might initially assume that most adults are approximately 5.5 feet tall.
, represents any assumptions you have before observing the actual data. For instance, you might initially assume that most adults are approximately 5.5 feet tall. - Likelihood: The likelihood distribution, denoted as
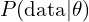 , measures how well a particular parameter explains the observed data. For example, if you observe a person’s shoe size(eg: shoe size of 10), it might indicate that they are likely taller than 6 feet.
, measures how well a particular parameter explains the observed data. For example, if you observe a person’s shoe size(eg: shoe size of 10), it might indicate that they are likely taller than 6 feet. - Posterior: The posterior distribution, denoted as
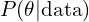 , represents how your initial assumptions are updated based on the observed data. For example, combining your prior belief that most adults are around 5.5 feet tall with the observed shoe size data, you now estimate that the person is likely 6 feet tall.
, represents how your initial assumptions are updated based on the observed data. For example, combining your prior belief that most adults are around 5.5 feet tall with the observed shoe size data, you now estimate that the person is likely 6 feet tall.
MCMC helps sample from the posterior to refine this estimate. To understand this in detail checkout this article.
What is Prior, Likelihood and Posterior in 3DGS?
In a Bayesian view of 3D Gaussian Splatting (3DGS), you can interpret the model parameters (the positions, sizes, colors, opacities, etc. of all the Gaussian splats) as random variables. Then:
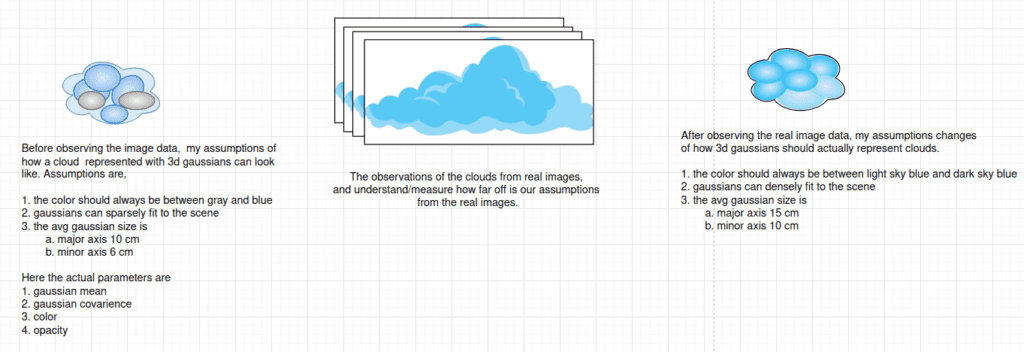
- A prior distribution over those parameters,
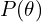 , encodes any assumptions or preferences you have before seeing the actual image data. For instance, you might prefer that your Gaussians not be unbounded in size, or that their colors lie in a reasonable range, or that the total number of splats not explode, etc.
, encodes any assumptions or preferences you have before seeing the actual image data. For instance, you might prefer that your Gaussians not be unbounded in size, or that their colors lie in a reasonable range, or that the total number of splats not explode, etc.
- A likelihood
 measures how well a particular configuration
measures how well a particular configuration 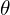 of splats explains the actual observed images (the training views).
of splats explains the actual observed images (the training views).
- The posterior distribution is then

In words ![]() is, how your initial assumptions get updated by the observed image data.
is, how your initial assumptions get updated by the observed image data.
Only Convergence Vs Convergence + Exploration
Adaptive Density Control (ADC) is a heuristic approach that addresses the problem but is not fully optimized and lacks a solid mathematical foundation. MCMC tackles the same core issue by providing a stronger mathematical basis for densification and pruning strategies.
How does it achieve this? It introduces a probabilistic framework to these strategies by conceptualizing them as a sampling process.
“Sampling is a way to estimate the overall characteristics of a large group by studying just a small part of it.”
For example, imagine you need to find the area under a curve (as shown in the image below). Calculating it through integration might involve dealing with a complex formula. Instead, using the Monte Carlo method, you can randomly scatter red dots within a rectangle that bounds the curve. The more dots you use, the more accurate the estimate becomes. By calculating the ratio of dots that land under the curve to the total dots in the rectangle, you can determine the area under the curve, since the ratio corresponds to the proportion of the rectangle’s area.”

The general approach in 3DGS has been:
- Finding a single best solution: 3DGS follows a straightforward optimization approach. It initializes the Gaussians and then optimizes their configuration by calculating the L1 loss between the rendered image and the ground truth image. This loss is used to update the Gaussians. However, this method tends to produce a single best solution and can suffer from the issue of getting stuck in local minima.
MCMC proposes a different approach, instead of focusing on finding a single best solution, it aims to identify a range of configurations that explain the data equally well by sampling from the posterior distribution.
MCMC for Probabilistic 3DGS Modeling
MCMC introduces a posterior distribution ![]() , which represents the probability of a Gaussian configuration
, which represents the probability of a Gaussian configuration ![]() (positions, colors, shapes, etc.) being correct given the training data. In other words:
(positions, colors, shapes, etc.) being correct given the training data. In other words:
![]()
Here, ![]() and
and ![]() refer to the same configuration.
refer to the same configuration.
This distribution ![]() is designed such that configurations of
is designed such that configurations of ![]() that represent the scene well will have higher values of
that represent the scene well will have higher values of ![]() , while configurations that poorly represent the scene will have lower values.
, while configurations that poorly represent the scene will have lower values.
By turning the problem into sampling from a distribution, they can use a Markov Chain Monte Carlo (MCMC) method (like Stochastic Gradient Langevin Dynamics (SGLD)) to generate a sequence of parameter states ![]() . Under the right conditions, this Markov chain will produce samples that reflect how likely each
. Under the right conditions, this Markov chain will produce samples that reflect how likely each ![]() is under
is under ![]() .
.
The authors use Stochastic Gradient Langevin Dynamics (SGLD) as the MCMC framework. As the name suggests, it combines two components: Stochastic Gradient and Langevin Dynamics. Stochastic Gradient Langevin Dynamics (SGLD) operates similarly to regular gradient descent, but with an added stochastic noise component.
Stochastic Gradient Descent Updates
The gradient descent used here differs slightly; instead of calculating the loss over a batch of images, it computes the loss for a single image. For example, when updating a single Gaussian g in 3DGS with a learning rate of ![]() , the process reflects this unique approach.
, the process reflects this unique approach.

A more simple form would be,

One important component missing in the above equation is ![]() . This term represents the expectation over the training set
. This term represents the expectation over the training set ![]() . It involves randomly sampling an image
. It involves randomly sampling an image ![]() from the pool of images in the training set and calculating the loss based on that sample.
from the pool of images in the training set and calculating the loss based on that sample.
While the equation suggests that the total loss is calculated as the average loss across all images in the training set, the implementation takes a different approach. In the code, the model computes the loss for a single randomly selected image at a time and updates the parameters accordingly.
Stochastic Gradient Langevin Dynamics Explained
The SGLD update described in the paper goes like this,

![]() represents the posterior distribution of the random variable g, conditioned on the data, while
represents the posterior distribution of the random variable g, conditioned on the data, while ![]() represents the noise. The role of
represents the noise. The role of ![]() is to explore the parameter space of the Gaussians (e.g., positions, opacities, covariances, etc.). This exploration is beneficial because:
is to explore the parameter space of the Gaussians (e.g., positions, opacities, covariances, etc.). This exploration is beneficial because:
- Avoiding local minima.
- Generating multiple solutions for Gaussian configurations, which helps provide a more comprehensive representation of the scene.
![]() and
and ![]() control the trade-off between convergence speed and exploration.
control the trade-off between convergence speed and exploration.
The goal of the above equation is to maximize the likelihood, as a higher likelihood indicates a better fit to the data. Simultaneously, it aims to explore the parameter space sufficiently to avoid getting stuck in local minima.
Connecting SGD and SGLD to MCMC
Now comes the important part where the connection to the MCMC logic is established. By comparing the equations for SGD and SGLD, you can see that:

If you simplify more,

The above equation can also be represented as,

As the total loss is divided into two parts,
- How well the Gaussians reconstruct the images
- Any additional regularization terms in
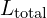
And if we put ![]() and
and ![]() we get back to the standard Gaussian splatting parameter updation equation.
we get back to the standard Gaussian splatting parameter updation equation.
Modified SGLD Used in the Paper
The exact SGLD equation is not directly used for updates. Instead, the authors modify it by retaining the standard SGD update and adding a noise term with a coefficient ![]() . Rather than using plain SGD, they employ the Adam optimizer with its default parameters.
. Rather than using plain SGD, they employ the Adam optimizer with its default parameters.

Through various experiments, the authors discovered that exploration is unnecessary for opacity, scale, and color. Therefore, they only add noise to the mean/center of the Gaussians.
Defining the Noise Term
The noise term ![]() is a function of a sigmoid centered at the opacity difference
is a function of a sigmoid centered at the opacity difference ![]() , scaled by the Gaussian’s covariance
, scaled by the Gaussian’s covariance ![]() , steepness defined by
, steepness defined by ![]() and modulated by the learning rate
and modulated by the learning rate ![]() .
.

![]() is a random noise vector sampled from a multivariate Gaussian distribution with a mean of 0 and a covariance matrix
is a random noise vector sampled from a multivariate Gaussian distribution with a mean of 0 and a covariance matrix ![]() (identity matrix). The size of the noise vector matches the number of Gaussians in the scene.
(identity matrix). The size of the noise vector matches the number of Gaussians in the scene.

![]() represents the sigmoid function, with
represents the sigmoid function, with ![]() and
and ![]() as hyperparameters that control its sharpness. These are set to
as hyperparameters that control its sharpness. These are set to ![]() = 100 and
= 100 and ![]() =(1−0.005)=0.995, creating a sharp transition function that quickly transitions from zero to one.
=(1−0.005)=0.995, creating a sharp transition function that quickly transitions from zero to one.
The noise is applied only to Gaussians with opacity below 0.995, meaning it has no effect on highly opaque(high opacity) Gaussians. This is logically sound because a Gaussian with an opacity greater than 0.995 is likely already in a proper configuration that contributes effectively to representing the scene. Therefore, only Gaussians with opacity below 0.995 need to be updated.

Lets discuss how is this implemented in code,
# Optimizer step
if iteration < opt.iterations:
gaussians.optimizer.step()
gaussians.optimizer.zero_grad(set_to_none = True)
L = build_scaling_rotation(gaussians.get_scaling, gaussians.get_rotation)
actual_covariance = L @ L.transpose(1, 2)
def op_sigmoid(x, k=100, x0=0.995):
return 1 / (1 + torch.exp(-k * (x - x0)))
noise = torch.randn_like(gaussians._xyz) * (op_sigmoid(1 - gaussians.get_opacity))*args.noise_lr*xyz_lr
noise = torch.bmm(actual_covariance, noise.unsqueeze(-1)).squeeze(-1)
gaussians._xyz.add_(noise)
- if the current iteration is less than the total number of training iterations specified in opt.iterations, gaussians.optimizer.step() performs a standard optimization step using the Adam optimizer.
- gaussians.optimizer.zero_grad(set_to_none = True) : Resets the gradients of all optimized parameters in the gaussians model to zero before the next iteration.
set_to_none = Trueis a memory optimization in PyTorch. - L = build_scaling_rotation(gaussians.get_scaling, gaussians.get_rotation): This line calculates a matrix L representing the combined scaling and rotation for each Gaussian, using the current scaling and rotation parameters from the gaussians model.
- actual_covariance = L @ L.transpose(1, 2): Computes the actual covariance matrix for each Gaussian by multiplying the L matrix with its transpose.
- op_sigmoid: This function used to modulate the noise based on Gaussian opacity. k controls the sharpness, and x0 centers the transition.
- noise = torch.randn_like(…): This line generates random noise for each Gaussian’s position (_xyz).
- noise = torch.bmm(actual_covariance, noise.unsqueeze(-1)).squeeze(-1): This line transforms the isotropic noise (from
randn_like) into anisotropic noise. It multiplies the noise by theactual_covariancematrix, shaping the noise according to each Gaussian’s shape and orientation. - gaussians._xyz.add_(noise): This line adds the generated and transformed noise to the _xyz attribute of the gaussians model.
From the above code, you can find the similarity between the code and the equations provided in the paprt.
MCMC Densification and Pruning Strategies
The configuration of Gaussians is defined as g, also referred to as a sample state. When the configuration is updated, g changes accordingly.
The 3D Gaussian Splatting heuristics involve operations such as ‘move,’ ‘split,’ ‘clone,’ ‘prune,’ and ‘add’ Gaussians, which encourage more “live” Gaussians (![]() ). Changing these heuristics transitions the system from one sample state (
). Changing these heuristics transitions the system from one sample state (![]() ) to another (
) to another (![]() ).
).
However, such transitions can potentially collapse the entire MCMC sampling process. To address this issue, the authors impose a condition: the states can only change if ![]() .
.
Previously, we observed that ![]() represents the negative log-likelihood or the total loss. This implies that a state update can only occur if the loss of the old state is equal to the loss of the new state.
represents the negative log-likelihood or the total loss. This implies that a state update can only occur if the loss of the old state is equal to the loss of the new state.
The process of state update or transition is described below:
- Move “dead” to “live”: All dead Gaussians (
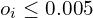 ) are relocated to the positions of live Gaussians.
) are relocated to the positions of live Gaussians. - The parameters of the relocated dead Gaussians are updated to minimize their impact on the rendered images.
- For example, if you want to update
 dead Gaussians (
dead Gaussians ( ) to align with a live Gaussian (
) to align with a live Gaussian ( ), parameters such as mean, covariance, and opacity are updated as follows:
), parameters such as mean, covariance, and opacity are updated as follows:

From the above equation you can observe,
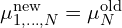 : new means
: new means 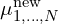 of all the dead Gaussians being relocated are set to the mean (
of all the dead Gaussians being relocated are set to the mean (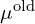 ) of the live Gaussian.
) of the live Gaussian.![o_i^{\text{new}} = 1 - \sqrt[N]{1 - o_N^{\text{old}}}](https://learnopencv.com/wp-content/ql-cache/quicklatex.com-7f3f3f8c5ab1657bb45ba202ae7069ef_l3.png) : This formula redistributes the opacity contributions of the dead Gaussians being moved to match the original rendering contribution. The use of the N-th root ensures a balanced redistribution when multiple Gaussians are involved.
: This formula redistributes the opacity contributions of the dead Gaussians being moved to match the original rendering contribution. The use of the N-th root ensures a balanced redistribution when multiple Gaussians are involved.- In the 3rd equation, each relocated Gaussian
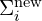 is scaled to account for the change in opacity. The scaling factor ensures the combined effect of the N−1 relocated Gaussians equals the original rendering contribution of
is scaled to account for the change in opacity. The scaling factor ensures the combined effect of the N−1 relocated Gaussians equals the original rendering contribution of 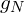 .
.
Although the proposed MCMC densification and pruning strategies may appear similar to the original 3D Gaussian Splatting approach, the MCMC strategy is significantly more robust. This robustness becomes evident when comparing the original method and the center-corrected approach to the MCMC method.

The image above illustrates a 1D example of rasterizing a Gaussian with an opacity of 0.95, followed by rasterizing it as four cloned Gaussians using different strategies. Observe the rasterization results before and after cloning.
Although the method achieves ![]() , it is not exact. To minimize disruptions during training, the move is applied every 100 iterations. A target Gaussian is selected for movement using multinomial sampling, with live Gaussians chosen based on probabilities proportional to their opacity values.
, it is not exact. To minimize disruptions during training, the move is applied every 100 iterations. A target Gaussian is selected for movement using multinomial sampling, with live Gaussians chosen based on probabilities proportional to their opacity values.
Loss Function
The final loss function remains the same as in 3DGS, with the addition of regularization terms applied to covariance and opacity, as these parameters effectively determine the existence of a Gaussian. These are referred to as scale regularization and opacity regularization, respectively. The equation is shown below:
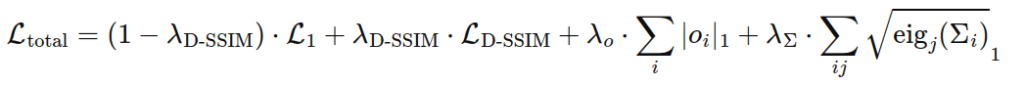
Here, ![]() denotes the j-th eigenvalues of the covariance matrix.
denotes the j-th eigenvalues of the covariance matrix.
Implement Object Insertion in Gaussian Splatting
The objective of this article is to perform object insertion while ensuring that both the scene and the object splats are free of floaters. However, when tackling this problem, you will typically encounter the following challenges:
- Generating a floater-free, high-fidelity scene.
- Creating splats for the object to be inserted without including the background.
- Scaling and positioning the object splats appropriately within the larger scene.
The standard 3DGS approach is insufficient because it inherently generates floaters to compensate for exposure or color variations. These floaters are generally difficult to eliminate using traditional outlier removal methods. To address this, we will use 3DGS with MCMC combined with Bilateral Grids.
3DGS MCMC effectively converges faster and removes floaters from the scene. For this process, we will use the gsplats library from NeRFStudio to train the scene with MCMC. For individual objects, however, we will rely on the INRIA Gaussian Splatting repository.
We will use the Garden dataset for these experiments, along with a few additional object captured in our office. Use the commands below to download the datasets.
$ wget http://storage.googleapis.com/gresearch/refraw360/360_v2.zip
$ wget https://www.dropbox.com/scl/fi/2k5xfxpani744dzbxco5h/obj_insert_canvas_data_blog.zip?rlkey=pxwui6w4h7s8ql3eqpxzq51ls&st=8fl2f5f1&dl=1
The mipNeRF360 dataset already includes the COLMAP output, so we won’t need to run COLMAP this time. If you’re working with a custom dataset, I recommend referring to the previous article on Gaussian Splatting, which provides a detailed guide on how to set it up.
Training Scene Splat
You can train the garden scene very easily using the below command,
$ CUDA_VISIBLE_DEVICES=0 python examples/simple_trainer.py mcmc \
--use_bilateral_grid \
--data_dir /path/of/garden/folder \
--result_dir /path/to/result/garden \
--data_factor 1
The simple_trainer.py script is usually run with the default flag, but since we are using 3DGS MCMC, we need to set the mcmc flag along with the --use_bilateral_grid flag to enable the bilateral grid.
--data_dir: This is the directory where the images and sparse folders are located.--result_dir: Specify an empty directory to store the results. I recommend creating a directory named results and, inside it, another folder named garden to organize the output.--data_factor: This refers to the resolution at which 3DGS processes your images. A value of 1 retains the original resolution.
Training Object Splat
Now, let’s train the 3D Gaussian Splatting model for the objects. We will use the INRIA codebase to train the objects with masks, specifically RGBA images. The method is to use the COLMAP on the original image but run 3DGS on the masked out RGBA images. We will be using the default 3DGS to train the object splat. After running the colmap, go to Reconstruction -> Dense Reconstruction -> Select the workspace (ignore if already selected) -> Undistortion.
You can use models like Segment Anything or other segmentation models trained on specific classes for background removal. However, in this case, we will use the rembg library to remove the background from images.
To get started, install the rembg library by following the instructions provided in its GitHub repository. Once installed, run the command below:
$ rembg p /path/to/object/images /path/to/object/images_rembg
We have been using .png images directly, but it throws an error because the system is trying to locate .jpg images. You can either modify the code to accept .png images or convert the .png images to .jpg format with a white background.
Once you have removed the background, you will have RGBA images. To convert these images to .jpg format with a white background, run the command below:
$ cd /path/to/object/images_rembg
$ for file in *.png; do convert "$file" -background white -flatten "${file%.png}.jpg"
$ mv /path/to/object/images /path/to/object/images_org
$ mv /path/to/object/images_rembg /path/to/object/images
I have experimented this mask guided splatting approach on NeRF-Studio also but the initial results were not good, though I believe that there are ways to achieve that using that library.
Use below command to train on the canvas dataset,
$ python train.py -s /path/to/canvas/folder \
-m /path/to/results/folder \
--white_background
This command is similar to the gsplats command, but we are using three specific flags:
-s: Equivalent to--data_dir.-m: Equivalent to--result_dir.--white_background: Ensures the background is removed from the splat of the object.
After running the command, you will find the .ply files in the results folder.
Removing Outliers from 3D Gaussian Splatting
These .ply files may still contain some white splats hanging around, but these can be easily removed using the 3dgsconverter library.
To use it:
- Install the library by following the instructions on the GitHub repository.
- Once installed, you can directly run the commands below:
$ 3dgsconverter -i input_3dgs.ply -o output_cc.ply -f cc --remove_flyers
$ 3dgsconverter -i output_cc.ply -o output_3dgs.ply -f 3dgs
By default, the --remove_flyers option uses the radius outlier removal algorithm to eliminate outliers. The default parameters are 25 for the number of neighbors and 10.5 for the threshold factor. You can adjust these values to achieve better results.
Merge Object and Scene Splats
Now that the Gaussian splats for both the object and the scene are prepared, the next step is to insert the object into the scene. For this, we will use the script provided below.
#!/usr/bin/env python3
# insert_canvas_in_garden.py
import os
import torch
import numpy as np
from plyfile import PlyData, PlyElement
from dataclasses import dataclass
from scipy.spatial.transform import Rotation as R
from typing import List
class GsData:
def __init__(self):
self.sh_degrees: int
self.xyz: np.ndarray # [n, 3]
self.opacities: np.ndarray # [n, 1]
self.features_dc: np.ndarray # ndarray[n, 3, 1], or tensor[n, 1, 3]
self.features_rest: np.ndarray # ndarray[n, 3, 15], or tensor[n, 15, 3]; NOTE: this is features_rest actually!
self.scales: np.ndarray # [n, 3]
self.rotations: np.ndarray # [n, 4]
def qvec2rotmat(self, qvec):
...
def rotmat2qvec(self, R):
...
def quat_multiply(self, quaternion0, quaternion1):
...
def transform_shs(self, features, rotation_matrix):
...
def load_array_from_plyelement(self, plyelement, name_prefix: str, required: bool = True):
names = [p.name for p in plyelement.properties if p.name.startswith(name_prefix)]
names = sorted(names, key=lambda x: int(x.split('_')[-1]))
v_list = [np.asarray(plyelement[attr_name]) for idx, attr_name in enumerate(names)]
return np.stack(v_list, axis=1)
# @lp
def load_from_ply(self, ply_file_path: str):
plydata = PlyData.read(ply_file_path)
vertex = plydata['vertex'].data
self.sh_degrees = 3
self.xyz = np.vstack([vertex['x'], vertex['y'], vertex['z']]).T
self.opacities = np.asarray(plydata.elements[0]["opacity"])[..., np.newaxis]
self.features_dc = np.vstack([plydata.elements[0]["f_dc_0"],
plydata.elements[0]["f_dc_1"],
plydata.elements[0]["f_dc_2"]]).T[..., np.newaxis]
self.features_rest = self.load_array_from_plyelement(plydata.elements[0],
"f_rest_", required=False).reshape((self.xyz.shape[0],
self.sh_degrees, -1))
self.scales = self.load_array_from_plyelement(plydata.elements[0], "scale_") #scale
self.rotations = self.load_array_from_plyelement(plydata.elements[0], "rot_") # quatenion
def rescale(self, factor:float):
self.xyz = self.xyz * factor
# self.scales = self.scales * factor
self.scales += np.log(factor)
def save_to_ply(self, path: str, with_colors: bool = False):
# os.makedirs(os.path.dirname(path), exist_ok=True)
xyz = self.xyz
normals = np.zeros_like(xyz)
f_dc = self.features_dc.reshape((self.features_dc.shape[0], -1))
if self.sh_degrees > 0:
f_rest = self.features_rest.reshape((self.features_rest.shape[0], -1))
else:
f_rest = np.zeros((f_dc.shape[0], 0))
opacities = self.opacities
scale = self.scales
rotation = self.rotations
def construct_list_of_attributes():
attributes = ['x', 'y', 'z', 'nx', 'ny', 'nz']
attributes += [f'f_dc_{i}' for i in range(f_dc.shape[1])]
if self.sh_degrees > 0:
attributes += [f'f_rest_{i}' for i in range(f_rest.shape[1])]
attributes += ["opacity"]
attributes += [f'scale_{i}' for i in range(scale.shape[1])]
attributes += [f'rot_{i}' for i in range(rotation.shape[1])]
return attributes
dtype_full = [(attribute, 'f4') for attribute in construct_list_of_attributes()]
attribute_list = [xyz, normals, f_dc, f_rest, opacities, scale, rotation]
if with_colors:
from sh_utils import eval_sh
rgbs = np.clip(eval_sh(0, self.features_dc, None) + 0.5, 0.0, 1.0)
rgbs = (rgbs * 255).astype(np.uint8)
dtype_full += [('red', 'u1'), ('green', 'u1'), ('blue', 'u1')]
attribute_list.append(rgbs)
elements = np.empty(xyz.shape[0], dtype=dtype_full)
attributes = np.concatenate(attribute_list, axis=1)
elements[:] = list(map(tuple, attributes))
el = PlyElement.describe(elements, 'vertex')
PlyData([el]).write(path)
def rotate(self, rpy: List):
rot = R.from_euler('xyz', rpy)
quaternion = rot.as_quat()
rot_mat = self.qvec2rotmat(quaternion)
# Apply rotation to points
self.xyz = (rot_mat @ self.xyz.T).T
# Update rotations using quaternion multiplication
self.rotations = torch.nn.functional.normalize(
torch.from_numpy(self.quat_multiply(self.rotations,
quaternion))).numpy()
# Transform SH coefficients
features = np.concatenate((self.features_dc, self.features_rest),
axis=2).transpose((0, 2, 1))
features = self.transform_shs(features, rot_mat)
self.features_rest = features[:, 1:, :].transpose((0, 2, 1))
def translation(self, x: float, y: float, z: float):
if x == 0. and y == 0. and z == 0.:
return
# Apply translation after rotation
self.xyz = self.xyz + np.array([x, y, z])
def deg2rad(self, rpy_deg):
return [(np.pi/180) * i for i in rpy_deg]
This is the code that is used to read, rescale and position the object splat to the bigger scene and finally merge both the scenes into one single ply file. We will not go over all of them, but only the important ones.
- load_from_ply:
Reads a PLY file to load vertex attributes such as positions, features, scales, and rotations into the class attributes. This function parses the file and organizes its data for efficient manipulation, making it a cornerstone for initializing the data for further transformations. - rescale:
Adjusts the scale of the spatial positions by multiplying them with a factor. It also logarithmically adjusts the scales, allowing for efficient scaling transformations while preserving proportional dimensions in the dataset. - save_to_ply:
Saves the current state of the data, including positions, features, and other attributes, back to a PLY file format. This function allows users to store and visualize the transformed data. It optionally computes and adds color attributes based on spherical harmonics for better visualization. - rotate:
Applies a 3D rotation, defined by roll, pitch, and yaw, to the spatial positions and updates the quaternion-based rotation attributes. It also adjusts SH features to align with the new orientation. This ensures all data, including lighting or appearance, is consistent after rotation. - translation:
Moves the spatial positions by a specified offset in the x, y, and z directions. This allows for shifting the entire dataset within the 3D space, useful for aligning or repositioning objects relative to other elements.
if __name__ == "__main__":
base_obj_fdr = "path/to/obj/ply/folder"
base_scene_fdr = "/path/to/scene/ply/folder"
# Load and process the object PLY file
obj_path = os.path.join(base_obj_fdr, "canvas_3dgs.ply")
obj_gs_data = GsData()
obj_gs_data.load_from_ply(obj_path)
# Process object (scale and rotate)
scale_factor = 0.06
obj_gs_data.rescale(scale_factor)
rpy = [80, -180, 30] # -193 for y worked y-185, inc z - > rotates the obj like falling face first
rpy_rad = obj_gs_data.deg2rad(rpy)
obj_gs_data.rotate(rpy_rad)
x, y, z = 0.05, -0.3, 0.6 # z val -> high bring up obj # inc in y -> toward the center
obj_gs_data.translation(x,y,z)
# Load the scene PLY file
scene_path = os.path.join(base_scene_fdr, "garden_scene_3dgs.ply")
scene_gs_data = GsData()
scene_gs_data.load_from_ply(scene_path)
# Merge the data
# Concatenate all attributes
merged_gs = GsData()
# xyz = (1000000, 3) + (123196, 3) = (1123196, 3)
merged_gs.xyz = np.concatenate([scene_gs_data.xyz, obj_gs_data.xyz], axis=0)
# opacities = (1000000, 1) + (123196, 1) = (1123196, 1)
merged_gs.opacities = np.concatenate([scene_gs_data.opacities, obj_gs_data.opacities], axis=0)
# features_dc = (1000000, 3, 1) + (123196, 3, 1) = (1123196, 3, 1)
merged_gs.features_dc = np.concatenate([scene_gs_data.features_dc, obj_gs_data.features_dc], axis=0)
# features_rest = (1000000, 3, 15) + (123196, 3, 15) = (1123196, 3, 15)
merged_gs.features_rest = np.concatenate([scene_gs_data.features_rest, obj_gs_data.features_rest], axis=0)
# scales = (1000000, 3) + (123196, 3) = (1123196, 3)
merged_gs.scales = np.concatenate([scene_gs_data.scales, obj_gs_data.scales], axis=0)
# rotations -> (1000000, 4) + (123196, 4) = (1123196, 4)
merged_gs.rotations = np.concatenate([scene_gs_data.rotations, obj_gs_data.rotations], axis=0)
merged_gs.sh_degrees = scene_gs_data.sh_degrees # Assuming both have same SH degrees
# Save the merged result
output_path = os.path.join("process_3dgs_file", "garden_canvas_merged.ply")
merged_gs.save_to_ply(output_path, with_colors=True)
print(f"Original scene points: {len(scene_gs_data.xyz)}")
print(f"Object points: {len(obj_gs_data.xyz)}")
print(f"Merged points: {len(merged_gs.xyz)}")
print(f"Saved merged result to: {output_path}")
The code above demonstrates the process where we first read the object .ply file and apply scaling and positioning based on the provided rotation and translation values. Once that is done, we read the scene .ply file and concatenate all properties such as xyz, opacities, features_dc, scales etc., into another instance of the same class. Finally, we use the save_to_ply function to save the combined data into a .ply file. You can run it as follows,
$ python insert_canvas_in_garden.py
This approach allows us to directly operate on the Gaussian .ply file instead of converting it to a point cloud, performing the operations, and then converting it back to a Gaussian .ply file. This eliminates unnecessary back-and-forth conversions.
The output .ply file can be easily be visualized using the supersplat visualizer.

Key Takeaways
- MCMC Framework for Robustness: The Monte Carlo Markov Chain (MCMC) framework enhances the robustness of 3D Gaussian Splatting (3DGS) by addressing limitations in Adaptive Density Control (ADC) with a probabilistic approach, enabling better exploration and convergence.
- Object Insertion Challenges: Inserting objects into 3DGS requires overcoming challenges such as floater removal, precise scaling, and proper alignment of object splats within the scene, which are managed using MCMC with bilateral grids.
- Improved Training and Optimization: Stochastic Gradient Langevin Dynamics (SGLD) introduces noise into optimization, allowing the exploration of multiple solutions and avoiding local minima, which is crucial for high-fidelity reconstructions.
- Efficient Scene and Object Merging: The merging process directly operates on Gaussian splat attributes like positions, opacities, and scales, eliminating unnecessary conversions and enabling seamless integration of object splats into the scene.
Conclusion
This article demonstrates how 3D Gaussian Splatting with MCMC can overcome traditional limitations and achieve robust object insertion into scenes. By leveraging advanced probabilistic frameworks and efficient workflows, we can perform precise object positioning and generate photorealistic, floater-free scenes. The methods outlined here not only expand the applications of 3DGS but also set a foundation for future advancements in 3D computer vision and graphics.
References
- 3D Gaussian Splatting as Markov Chain Monte Carlo
- Bilateral Guided Radiance Field Processing
- INRIA Gaussian Splatting Repository
- NeRF-Studio Gsplat Repository








100K+ Learners
Join Free OpenCV Bootcamp3 Hours of Learning