3D Gaussian Splatting (3DGS) is redefining the landscape of 3D computer graphics and vision — but here’s a catch: it achieves groundbreaking results without relying on any neural networks, not even a small MLP! Gaussian splatting is used for high fedility 3D reconstruction of a scene. In “Gaussian Splatting”, “Gaussian” refers to the Gaussian distribution, bell-shaped normal probability distribution but, here it is being used as a primitive(basic or fundamental unit) to represent the 3D scene and “Splatting” refers to the process of projecting 3D points into a 2D image plane. A 3D model of a scene generated using 3D Gaussian splatting is highly photorealistic, accurately captures geometry, and enables real-time rendering. Unlike other existing solutions like MipNerf360, Plenoxels etc. Gaussian Splatting has the ability to capture larger scenes, with negligible artifacts/floaters.

Interesting facts, George Drettakis, co-author of 3DGS paper and senior researcher at INRIA gave a talk at Vincent Sitzmann’s lab(Scene Representation Group) at MIT CSAIL, where he mentioned,
- The biggest progress they made when they started using a visualizer to interact with the scene when it was being optimized. So, it’s very important to use visualization tools when working with these kinds of problem statements.
- The 1st author of the paper Bernhard Kerbl, is an expert in CUDA and GPU programming, in every weekly meeting he used to report that he made the implementation twice faster and he kept doing that for 3 months, which made the final implementation real-time.
The goal of this article is pretty straight forward, first we are going to understand the paper in-depth and understand all the equations. The Gaussian Splatting paper stands on the shoulders of many previous works that laid the groundwork for the concepts presented in it. So there are a lot of equations that’s being used directly, so understanding how they are derived or the intuition behind the equations are very important. And finally we will show how to use NeRF-Studio’s gSplat to train a gaussian splat on your custom data, and some guidance on how to get the best results.
Let’s dive in!
- Photogrammetry Vs NeRF Vs 3DGS
- Introduction to 3D Gaussian Splatting
- 3D Gaussian Splatting Projection
- Optimization
- Adaptive Control of Gaussians
- Training Pipeline
- Tile-based Rasterization of 3D Gaussians
- View-dependant Colors with Spherical Harmonics
- Train Gaussian Splatting on Custom Dataset
- Gaussian Splatting Limitations
- Key Takeaways
- Conclusion
Photogrammetry, NeRF and 3D Gaussian Splatting Comparison
3D reconstruction from multi-view has been a longstanding challenge in 3D vision and graphics! It involves generating a 3D representation of a scene based on a collection of 2D images taken from different viewpoints. The classical approach to solving this problem is photogrammetry. However, in 2020, Neural Radiance Fields (NeRFs) emerged as a more photo-realistic and robust alternative. Despite their advancements, NeRFs still had certain limitations, such as slow rendering time, artifacts/floaters, struggle to capture large scenes etc. Finally, in 2023, 3D Gaussian Splatting was introduced, addressing many of the issues NeRFs faced.

Photogrammetry
This problem has been initially tackled with 3D computer vision, with methods like Structure from Motion (SfM), Multi View Stereo (MVS) and Dense reconstruction. Generally these are feature based methods, which take the input image(s) and compute the feature points, then either track the points throughout the input sequence or compute feature points for the new frames and try to match with the previous frame feature points (these frames are called key-frames). These feature points are used to calculate the Essential matrix to get the camera pose and then use triangulation to get 3D points of the scene. Photogrammetry is generally slow rendering speed, struggles with reflective or transparent surfaces, reduced accuracy in texture-less environments and can have outlier 3D points but provides the highest geometric precision. We have a detailed article with code on Visual SLAM which is similar to SfM and MVS.
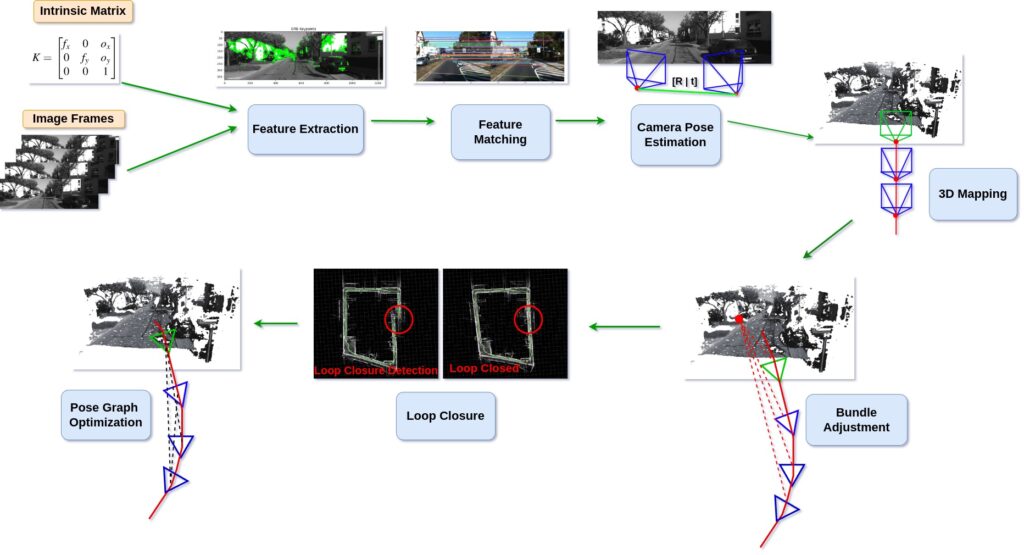
NeRF: Neural Radiance Fields
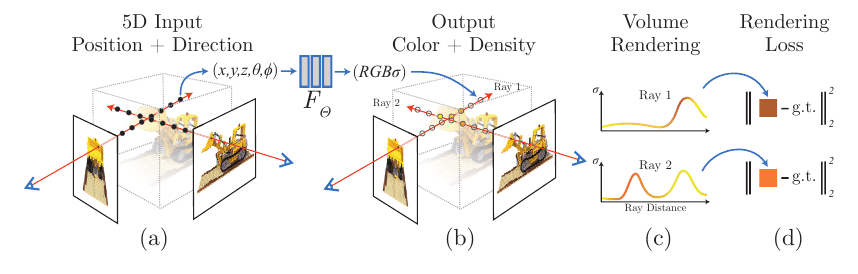
Neural Radiance Field (NeRF), is used for 3D reconstruction and novel-view synthesis, it’s an elegant idea, where a simple MLP neural network fused with volumetric rendering techniques to generate 3D scenes. It works on the concept of scene parameterization. In spite of being able to generate photo-realistic images and having geometric accuracy it struggles handling large-scale scenes and has slow rendering speed. We have an entire article dedicated on NeRF, going through its internal working and pytorch code.
3D Gaussian Splatting
3D Gaussian Splatting is a rasterization method that enables real-time rendering of photorealistic scenes learned from a limited set of images. For rasterization, instead of using triangles, it uses millions of Gaussian to represent the scene. The process begins by initializing a set of 3D Gaussians from a sparse point cloud generated by Structure-from-Motion (SfM). These gaussians are then optimized using adaptive density control, which refines distribution and alignment of the gaussians to better represent the scene. Finally a differentiable tile-based rasterizer is being used for efficient rendering, ensuring competitive training times compared to state-of-the-art radiance field methods. Once trained, the system allows real-time navigation and interaction with highly detailed and visually compelling 3D scenes.
No need to worry if terms, “adaptive density control”, “tile-based rasterizer” and others aren’t clear immediately — these concepts will be explained in more detail in the following sections.

Prefer listening? Check out the “PODCAST” version of this article.
3D Gaussian Splatting – An Introduction
The implementation of 3D Gaussian Splatting (3DGS) involves numerous elaborate steps that are essential for understanding how it works. Key aspects include:
- Projecting 3D Gaussians onto a 2D plane.
- Optimizing Gaussians to accurately capture the scene.
- Adaptive density control of 3D Gaussians
- Rendering 3D Gaussians onto a 2D image plane.
- Leveraging Spherical Harmonics to make 3DGS view-dependent.
This article serves as a comprehensive introduction for newcomers to 3D vision or graphics, providing a foundation to get started with 3D Gaussian Splatting. We will summarize the paper in detail, going over above mentioned points, walking through all the derivations and equations.
Let’s dive deep!
3D Gaussian Splatting Projection
Generally, 3D data is represented in one of three preferred ways: point clouds, meshes, or voxel grids. Among these, traditional rasterization methods often work with meshes, which typically use triangles as primitives to represent 3D scenes. Representing volumetric intricacies like hair, fur, or smoke often struggle when using triangles, and traditional rasterization methods often require substantial memory and computational resources to store and render large or highly detailed meshes.
To address these challenges, the authors needed a primitive that is both differentiable and capable of enabling very fast rendering. Authors chose 3D Gaussians, defined by a 3D covariance matrix ![]() and centered at a point (mean)
and centered at a point (mean) ![]() . These Gaussians are not only differentiable but can also be easily projected onto 2D splats, allowing efficient
. These Gaussians are not only differentiable but can also be easily projected onto 2D splats, allowing efficient ![]() -blending for rendering.
-blending for rendering.

Traditional Image Formation
Let’s consider that we’ve represented the 3D volume using 3D Gaussians. But once that’s done, how do we create a 2D render of the 3D scene? Well, the approach is same as how traditional image formation happens, which involves,
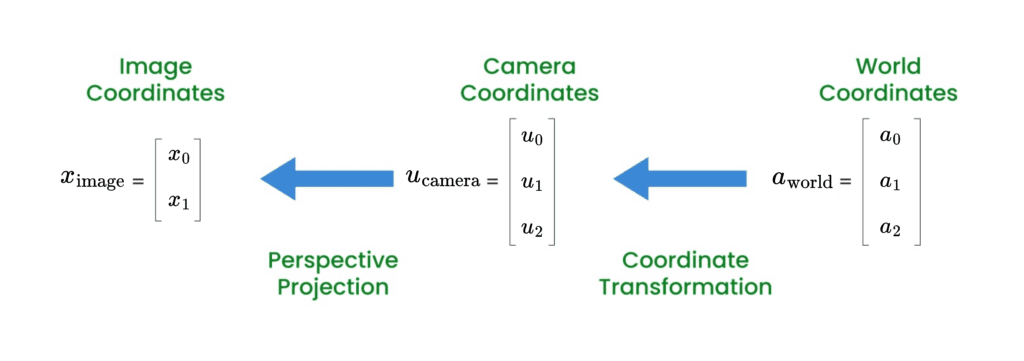
- Coordinate Transformation: The transformation from the world coordinate system (object space) to the camera coordinate system(camera space), it is done using the extrinsic matrix
![E_{\text{world}}^{\text{camera}} = [R \mid T],](https://learnopencv.com/wp-content/ql-cache/quicklatex.com-190fefd61e8163109e8863729164de2e_l3.png) which represents a linear (affine) transformation camera and world. Here,
which represents a linear (affine) transformation camera and world. Here, ![u_{camera} = [u_{0}, \ u_{1}, \ u_{2}]](https://learnopencv.com/wp-content/ql-cache/quicklatex.com-05ee6d9b8d45d12103c015ddf28ddb75_l3.png) , is a point in the camera’s coordinate system, while
, is a point in the camera’s coordinate system, while ![a_{world} = [a_{0}, \ a_{1}, \ a_{2}]](https://learnopencv.com/wp-content/ql-cache/quicklatex.com-b36f89d5c3f7c9b67504a01c9f468a4a_l3.png) is a point in the world or object coordinate system.
is a point in the world or object coordinate system.
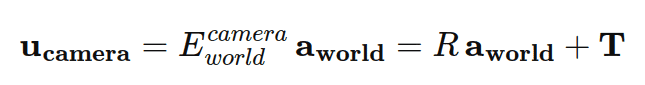
- Camera Projection: The transformation from 3D camera coordinates(object space) to 2D image coordinates (screen space) is performed using the intrinsic matrix
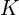 .
.  is made of the focal length and the optical centre(image centre coordinate,
is made of the focal length and the optical centre(image centre coordinate,  ).
).

Simple right! Very similar pipeline is applied on 3D gaussians, let’s see how!
3D to 2D Projection in Gaussian Splatting
Say, we need to project a 3D gaussian ![]() , in 2D. As mentioned above 1st step is the Affine transformation,
, in 2D. As mentioned above 1st step is the Affine transformation, ![]() , (where W is a 3X3 rotation matrix and P is a 1×3 translation vector), maps a 3D point
, (where W is a 3X3 rotation matrix and P is a 1×3 translation vector), maps a 3D point ![]() from object space to camera space. For a Gaussian Distributions:
from object space to camera space. For a Gaussian Distributions:
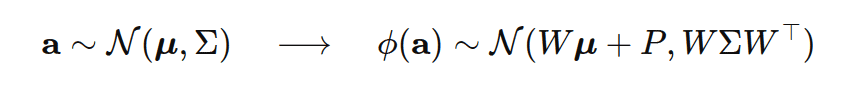
Here:
![u = \phi(a), = [u_0, u_1, u_2]^T](https://learnopencv.com/wp-content/ql-cache/quicklatex.com-35b272a915137647f589d4451573ec28_l3.png) , is a 3D point in camera coordinates.
, is a 3D point in camera coordinates.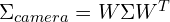 , Covariance matrix after affine transformation in camera space.
, Covariance matrix after affine transformation in camera space.
After this transformation, the camera projection is not applied immediately. Instead, there is an intermediate step called the Ray Space transformation, represented as ![]() . Note, that it’s still a 3D to 3D mapping. This Forward Rendering pipeline is introduced in the paper “EWA Volume Splatting“, where “EWA” stands for Elliptical Weighted Average.
. Note, that it’s still a 3D to 3D mapping. This Forward Rendering pipeline is introduced in the paper “EWA Volume Splatting“, where “EWA” stands for Elliptical Weighted Average.
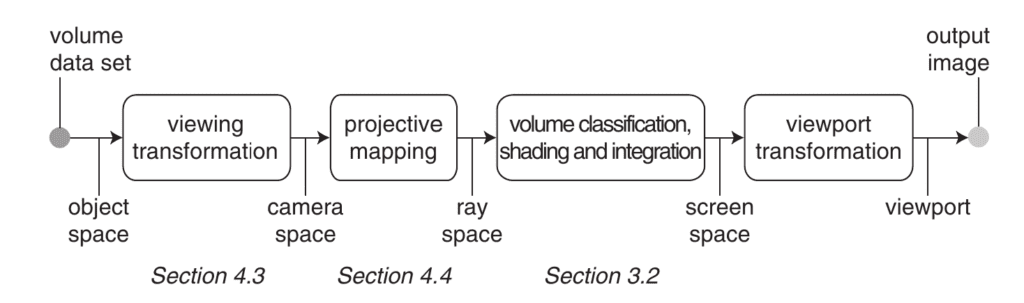
EWA volume splatting paper, introduces one additional space (coordinate system), called Ray Space, which aligning the rays parallel to a coordinate axis making it easier to integrate along the ray. Because of this we don’t have to do any sort of point sampling along a ray, which is done in NeRF. Final transformation from ray space to screen space involves creating the final rendered image with depth, color, and shading.
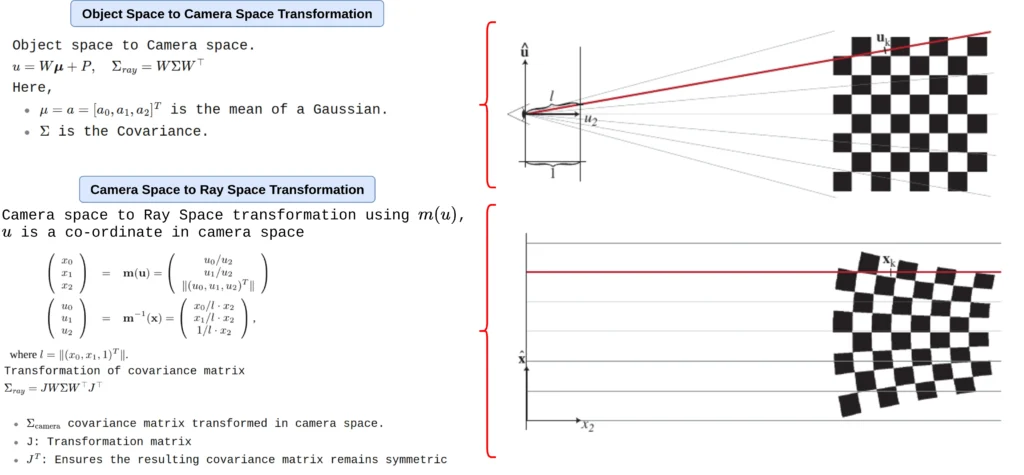
As you can see, this ray space transformation is non-linear, because of the division of horizontal and vertical components of the camera space coordinates based on the depth(![]() and
and ![]() ), so we can’t directly apply the affine transformation rules. Instead, we linearize
), so we can’t directly apply the affine transformation rules. Instead, we linearize ![]() around the mean
around the mean ![]() using a first-order Taylor expansion.
using a first-order Taylor expansion.
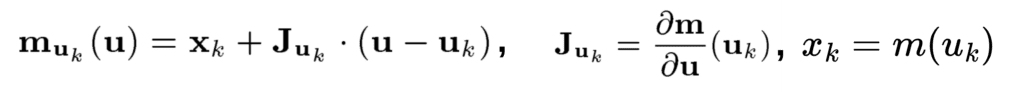
Where, ![]() or simply
or simply ![]() is the Jacobian of the local affine approximation
is the Jacobian of the local affine approximation ![]() , evaluated at
, evaluated at ![]() . For simplicity
. For simplicity ![]() subscript is removed.
subscript is removed.
Taylor Expansion Explained
A little bit refresher on Taylor expansion and Jacobian matrix. Taylor expansion is a mathematical tool for linear approximation of a nonlinear function around a specific point ![]() using a series of terms derived from the function’s derivatives.
using a series of terms derived from the function’s derivatives.
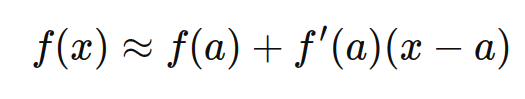
Here:
 : The value of the function at a, providing a constant term for the approximation.
: The value of the function at a, providing a constant term for the approximation.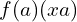 : The linear term, representing how the function changes with x near a.
: The linear term, representing how the function changes with x near a.
This effectively forms a straight line tangent to the function at ![]() , making it a local approximation that works well when x is close to a.
, making it a local approximation that works well when x is close to a.
The Jacobian matrix ![]() for the projection is derived by computing the partial derivatives of the camera coordinates with respect to the ray coordinates. The Jacobina involves focal length and image coordinates, for more understanding go through [3]. Note, that we are still in 3D.
for the projection is derived by computing the partial derivatives of the camera coordinates with respect to the ray coordinates. The Jacobina involves focal length and image coordinates, for more understanding go through [3]. Note, that we are still in 3D.
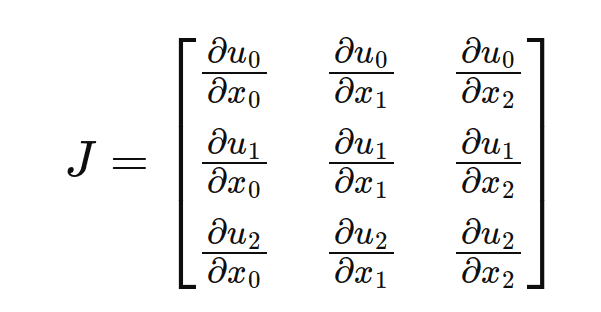
Covariance Matrix Transformation in Ray Space
We understand how the mean (a 3D point) changes after the ray space transformation (projective mapping). But what about the covariance matrix? how does it change after transforming from camera space to ray space? Well, it’s explained in the following sections,
- The 2D projection transforms the 3D Gaussian into 2D, The projected covariance
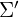 is:
is:
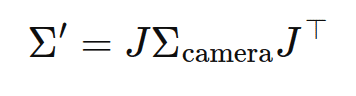
- Substitute
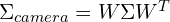 :
:
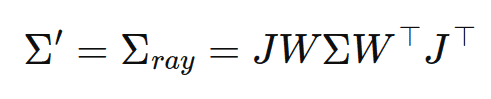
 represents the covariance matrix transformed from object space to camera space.
represents the covariance matrix transformed from object space to camera space.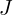 : Transforms used for ray space to screen space transformation.
: Transforms used for ray space to screen space transformation.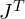 : Ensures the resulting covariance matrix remains symmetric (a key property of covariance matrices).
: Ensures the resulting covariance matrix remains symmetric (a key property of covariance matrices).
EWA volume splatting paper says that,
“Gaussians are closed under affine mappings and convolution, and integrating a 3D Gaussian along one coordinate axis results in a 2D Gaussian.”
So, if we skip the third row and column of ![]() , we obtain a 2×2 variance matrix(
, we obtain a 2×2 variance matrix(![]() ) with the same structure and properties as if we would start from planar points with normals.
) with the same structure and properties as if we would start from planar points with normals.
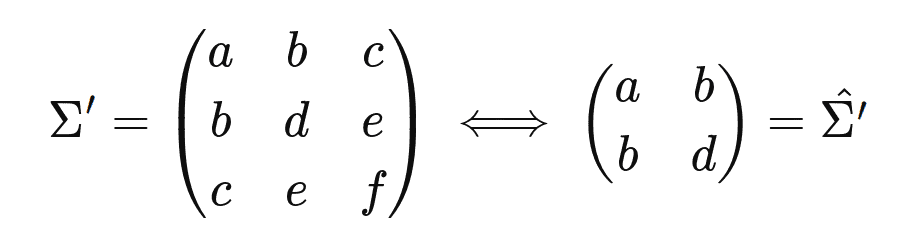
3D Gaussian to Ellipsoid
Covariance matrices only have physical meaning when they are positive semi-definite (PSD). However, for optimizing the covariance matrix (![]() ) to represent 3D Gaussians in the radiance field, the authors use gradient descent. This approach makes it challenging to ensure that the matrices remain valid, as update steps and gradients can easily produce invalid covariance matrices. So, how can we represent
) to represent 3D Gaussians in the radiance field, the authors use gradient descent. This approach makes it challenging to ensure that the matrices remain valid, as update steps and gradients can easily produce invalid covariance matrices. So, how can we represent ![]() in a way that guarantees it stays positive semi-definite during optimization?
in a way that guarantees it stays positive semi-definite during optimization?
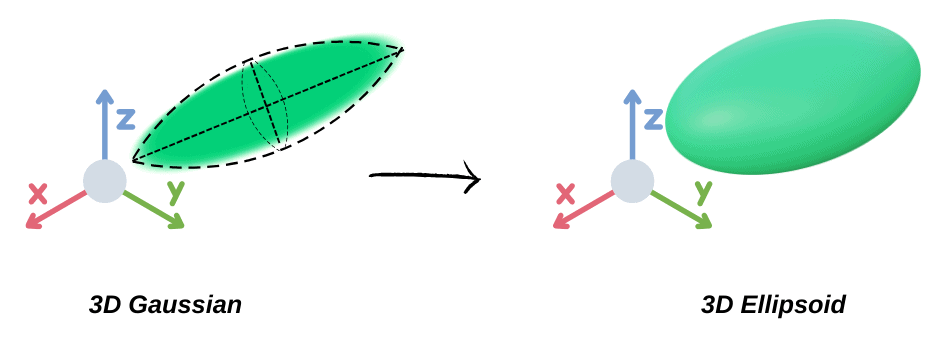
To solve this, the authors represent the 3D Gaussian as an 3D ellipsoid because the covariance matrix ![]() of a 3D Gaussian encodes the shape, size, and orientation which defines an ellipsoid in 3D space, where,
of a 3D Gaussian encodes the shape, size, and orientation which defines an ellipsoid in 3D space, where,
- The eigenvalues of
 determine the lengths of the ellipsoid’s principal axes.
determine the lengths of the ellipsoid’s principal axes. - The eigenvectors of
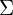 determine the orientation of these axes in 3D space.
determine the orientation of these axes in 3D space.
To maintain the Covariance matrix as PSD it is defined as,
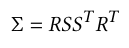
The covariance matrix ![]() can be decomposed as:
can be decomposed as: ![]() where:
where:
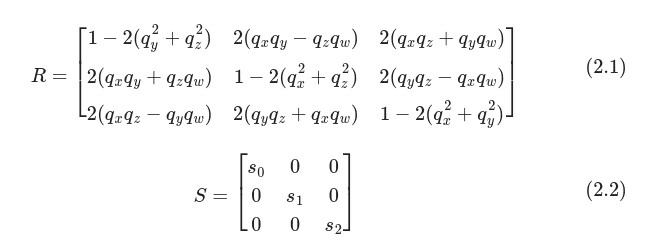
 : Diagonal matrix of eigenvalues (scaling the axes of the ellipsoid).
: Diagonal matrix of eigenvalues (scaling the axes of the ellipsoid). : Matrix of eigenvectors (orienting the ellipsoid).
: Matrix of eigenvectors (orienting the ellipsoid).
Instead of directly working with eigenvalues (![]() ), the authors use
), the authors use ![]() (a scaling matrix):
(a scaling matrix):
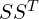 guarantees that the eigenvalues remain positive.
guarantees that the eigenvalues remain positive.- R controls the orientation of the ellipsoid.
Optimization
Above is the optimization pipeline of 3D gaussian splatting. The pipeline takes as input a sparse point cloud generated from SfM, along with the camera position and the corresponding image captured from that position. Each point is used to initialize the 3D gaussians. Apart from these, there are some more gaussians that are being initialized at other places in the volume randomly. After that Adaptive Density control is applied responsible for pruning and densification of the gaussians. After that’s done, we sample a camera position and its respective image and project the gaussians in a 2D image plane. Previously mentioned projection method and a tile based resterizer is used for rendering the image. This image and the image associated with the camera position are used to calculate the loss.
Here, author used stochastic gradient descent (Adam) for optimization, and the loss function is ![]() loss, combined with a D-SSIM term.
loss, combined with a D-SSIM term.
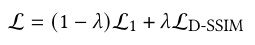
Differential-Structural Similarity Index Measure (D-SSIM), is an image similarity measure that takes Luminance, Contrast as well as Structural information into consideration.
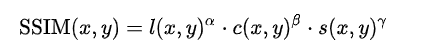
Here, ![]() is the Luminance,
is the Luminance, ![]() is Contrast and
is Contrast and ![]() is Structure. These terms are parameterized as,
is Structure. These terms are parameterized as,
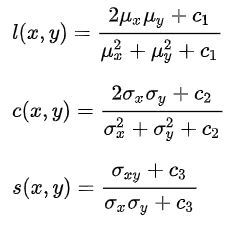
with:
 : the pixel sample mean of (x);
: the pixel sample mean of (x);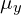 : the pixel sample mean of (y);
: the pixel sample mean of (y);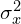 : the variance of (x);
: the variance of (x);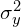 : the variance of (y);
: the variance of (y);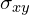 : the covariance of (x) and (y);
: the covariance of (x) and (y);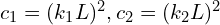 : two variables to stabilize the division with a weak denominator;
: two variables to stabilize the division with a weak denominator;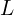 : the dynamic range of the pixel-values;
: the dynamic range of the pixel-values;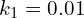 and
and 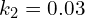 by default.
by default.
SSIM is better than other methods such as MSE(mean squared error) and PSNR (Peak signal-to-noise ratio) as they tend to estimate absolute error. To use SSIM as a loss term, it is reformulated into a differentiable loss function. One common approach is to use,
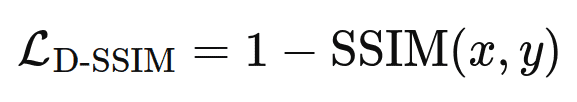
This ensures that minimizing ![]() maximizes the SSIM.
maximizes the SSIM.
The optimization tries to optimize 4 learnable parameters,
- Gaussian positions (
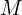 ),
), - Covariances (
 ),
), - Colors (
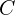 ), function of spherical harmonic(SH) parameters (discussed later)
), function of spherical harmonic(SH) parameters (discussed later) - Opacities (
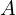 ) or transparency.
) or transparency.
So, after the loss calculation the gradients are being calculated for all of them and these parameters are being updated in the backward pass. Note that the optimization is happening in view space (2D image coordinate), not in world space. So the covariance (S or ![]() ) will be optimized for view space (
) will be optimized for view space (![]() ), and as we already know scaling (
), and as we already know scaling (![]() ) and rotation (
) and rotation (![]() ) are implicit components of the covariance matrix, so the optimization requires calculating gradients of the loss
) are implicit components of the covariance matrix, so the optimization requires calculating gradients of the loss ![]() with respect to
with respect to ![]() and
and ![]() indirectly,
indirectly,
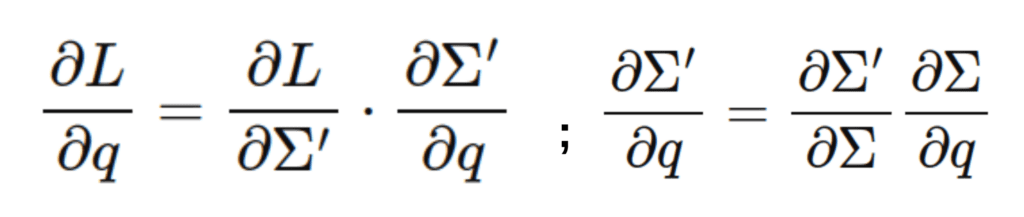
![]() reflects how
reflects how ![]() changes as scaling factors change.
changes as scaling factors change.
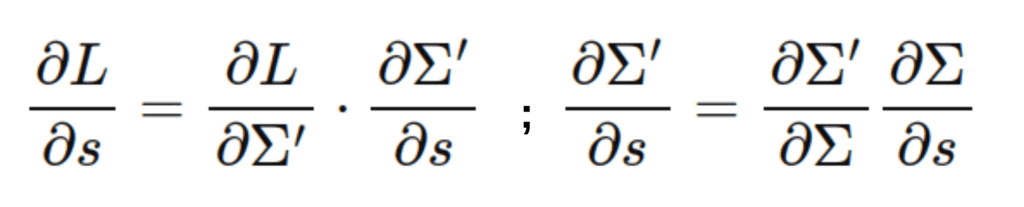
![]() reflects how
reflects how ![]() changes as the rotation (quaternion) changes. Directly computing
changes as the rotation (quaternion) changes. Directly computing ![]() and
and ![]() allows the algorithm to efficiently backpropagate gradients for scaling and rotation during optimization. Calculation details of this derivation is provided in the section “A DETAILS OF GRADIENT COMPUTATION” in the extra material.
allows the algorithm to efficiently backpropagate gradients for scaling and rotation during optimization. Calculation details of this derivation is provided in the section “A DETAILS OF GRADIENT COMPUTATION” in the extra material.
Now, that we have a clear understand of how the optmization pipeline works and diiferent components involved, lets go deep and understand
Adaptive Density Control
Adaptive Density Control is the method the authors came up with to dynamically adjust the number, density, and parameters of Gaussians to accurately and efficiently represent the 3D scene. This involves two steps,
- Pruning: If the opacity of is too small (
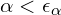 , here
, here 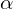 is the opacity or transparency of the gaussian and
is the opacity or transparency of the gaussian and 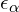 is the threshold) or the gaussian is too large, then it’s being removed.
is the threshold) or the gaussian is too large, then it’s being removed.
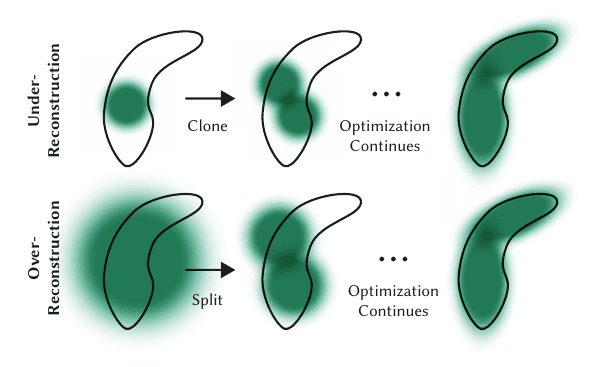
- Densification: This step handles two issue,
- Over-reconstruction: Over-reconstruction occurs when regions of a 3D scene are represented by excessively large or overlapping gaussians, leading to redundant and inefficient coverage of the geometry. To solve this the large gaussian is split in two parts (bottom row).
- Under-reconstruction: when regions of a 3D scene lack sufficient Gaussian coverage, resulting in missing or poorly represented geometric details. This is solved by merging/cloning two or more gaussians associated with the area (top row).
Training Pipeline
Now that we know how the optimization and densification works, let’s focus on how the training regime combines both of them to produce the final output.
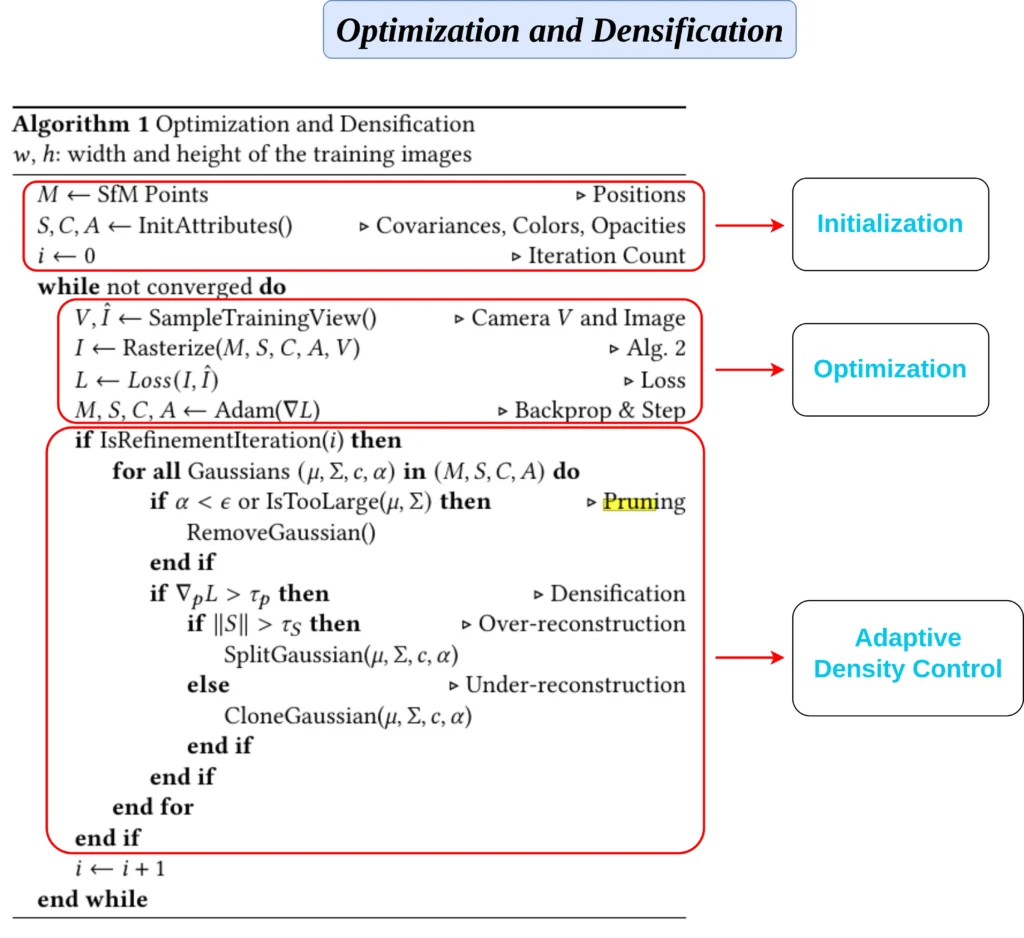
The algorithm takes structure from motion point cloud (![]() ), and using this the Covariance (
), and using this the Covariance (![]() ), Color(
), Color(![]() ) and Opacity(
) and Opacity(![]() ) of the gaussians are initialized. Note that the camera pose (including both position and orientation) is also obtained from Structure-from-Motion (SfM). Both the pose and the image captured from that specific pose are returned by the
) of the gaussians are initialized. Note that the camera pose (including both position and orientation) is also obtained from Structure-from-Motion (SfM). Both the pose and the image captured from that specific pose are returned by the SampleTrainingView() function.
In the training loop, we first resterize the 3D scene using the initialized parameters(![]() ) (
) (![]() is not mentioned) given
is not mentioned) given ![]() (camera pose), which results to a 2D image, which is being compared with the ground truth image (
(camera pose), which results to a 2D image, which is being compared with the ground truth image (![]() ), sampled using
), sampled using SampleTrainingView(). The Adam optimizer calculates the gradient of the learnable parameters and updates them.
Authors, perform pruning and densification every 100th iteration (if IsRefinementIteration(𝑖) then, checks if i equals to 100). If the transparency/opacity (![]() ) of a gaussian is too low, or the size of the gaussian is too large, it gets removed. If the positional gradient magnitude
) of a gaussian is too low, or the size of the gaussian is too large, it gets removed. If the positional gradient magnitude ![]() exceeds a threshold
exceeds a threshold ![]() , densification starts. In this process is gaussian’s scale or size (derived from its covariance matrix
, densification starts. In this process is gaussian’s scale or size (derived from its covariance matrix ![]() ) exceeds a threshold
) exceeds a threshold ![]() means its Over-reconstruction, and the gaussian need to be split (
means its Over-reconstruction, and the gaussian need to be split (SplitGaussian(𝜇, Σ, 𝑐, 𝛼)) else it’s Under-reconstruction, means that the gaussians need to be merged/cloned (CloneGaussian(𝜇, Σ, 𝑐, 𝛼)).
Can’t read right now? You can listen to the podcast version of this article instead.
Tile-based Rasterization of 3D Gaussians
First step of the resterizetion process is culling(CullGaussian(p, V)). Culling is the process where we eliminate Gaussians that are entirely outside the camera’s view frustum or in extreme positions where their contribution would be negligible. The view frustum is a 3D volume that defines the visible region of space for a camera. It is shaped like a truncated pyramid: – The near plane and far plane define the depth range. – The left, right, top, and bottom planes define the field of view (FOV).
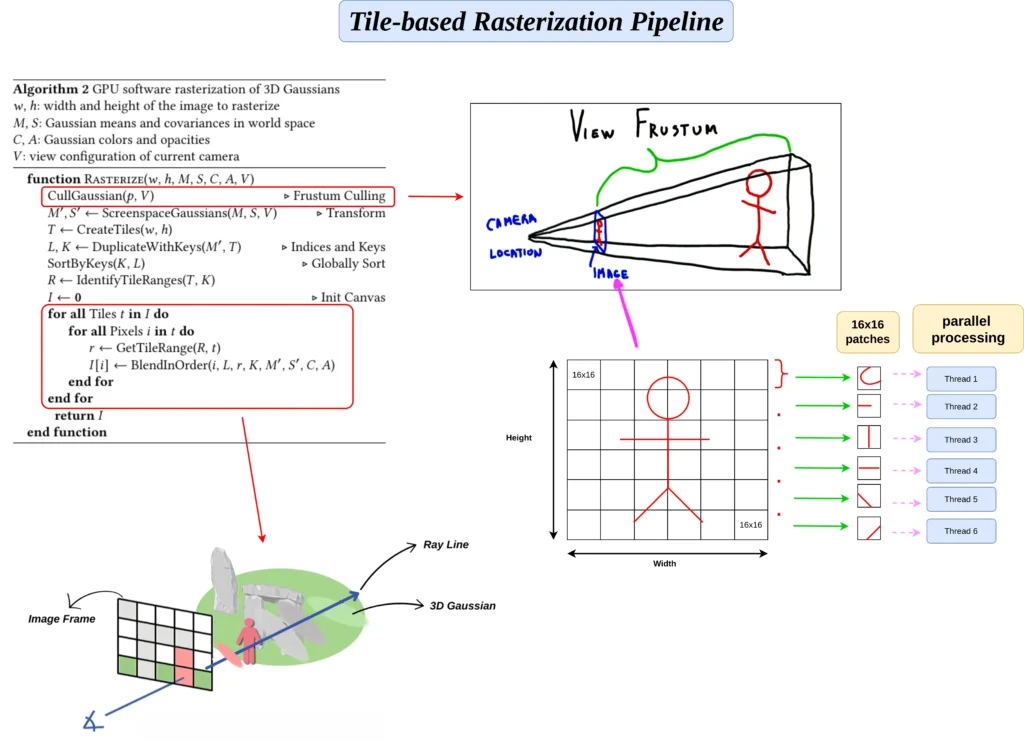
The function ScreenspaceGaussians(M,S,V), responsible for projecting the rest of the 3D gaussians to 2D image plane using the rendering method mentioned previously. The resulting ![]() and
and ![]() represent the Gaussian’s 2D position and footprint in the screen space.
represent the Gaussian’s 2D position and footprint in the screen space. CreateTiles(w, h) divides the screen into smaller regions (tiles) to enable efficient parallel processing. Each tile is a 16×16 pixel block. These tiles simplify Gaussian management and allow GPU threads to process them in parallel.
DuplicateWithKeys(M', T) duplicates gaussians for every tile they overlap and assigns them a key for sorting, the key combines depth and tile Id (Identifies which tile the Gaussian overlaps). A Gaussian splat’s projected ellipse (footprint) can span multiple screen tiles, so we duplicate the Gaussian for every intersected tile to ensure coverage. After that’s done, the gaussians are sorted (SortByKeys(K, L)) globally by their depth and tile ID using GPU Radix Sort. Sorting ensures that blending occurs front-to-back within each tile.
R ← IdentifyTileRanges(T, K) gives start and end indices in the sorted list of gaussians, belong to each tile after sorting.
Process each tile in parallel on the GPU, for each pixel in the tile, fetch the range of Gaussians affecting this tile, traverse the sorted Gaussians within the tile’s range and Compute its contribution to the pixel ![]() using its color (
using its color (![]() ) and opacity (
) and opacity (![]() ).
).
View-dependant Colors with Spherical Harmonics
Gaussian Splatting is View-dependent, and View-dependent means that the appearance (e.g., color, brightness) of an object changes based on the viewing direction relative to the object. Gaussian splatting adds the view-dependence feature using Spherical Harmonics(SH). Don’t worry we are not getting into quantum physics here. Instead of using RGB values for representing colors, Gaussian splatting uses SH to encode the color as a function of the viewing direction.
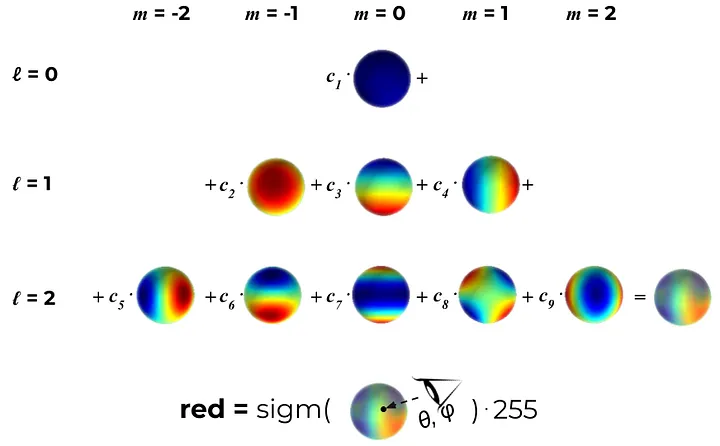
If you are not familiar with the concept of Spherical Harmonics, here is a refresher. Spherical Harmonics consists of two terms Spherical and Harmonics, to put it simply, Spherical Harmonics is a way of representing functions on the surface of a sphere(spherical coordinate system) using a series of harmonic (wave-like) basis functions. You might know, any 1D/2D periodic function/signal can be represented as a sum of sine and cosine waves, similarly in 3D, a combination of Spherical Harmonics are used to decompose functions defined on the surface of a sphere or on a spherical coordinate system.

Spherical Harmonic Function is parameterized by two integers, ![]() and
and ![]() ,
,
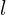 represents the number of azimuth or nodal lines (red strip)
represents the number of azimuth or nodal lines (red strip)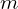 represents number of oscillations/variations
represents number of oscillations/variations
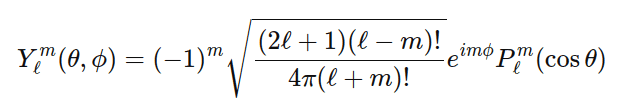
Given a ![]() number of nodal lines there will be
number of nodal lines there will be ![]() vibrations, see the below figure.
vibrations, see the below figure. ![]() are associated Legendre polynomials.
are associated Legendre polynomials. ![]() represents the oscillation function for a specific value of
represents the oscillation function for a specific value of ![]() and
and ![]() , given the viewing angle in terms of spherical coordinate system.
, given the viewing angle in terms of spherical coordinate system.
Here, ![]() are learned coefficients and instead of using a static RGB value, each channel is expressed as a linear combination of SH functions up to a maximum degree
are learned coefficients and instead of using a static RGB value, each channel is expressed as a linear combination of SH functions up to a maximum degree ![]() .
.
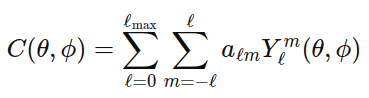
For ![]() = 1,
= 1, ![]() = 2 * 1 + 1 = 3 (from 0,1,2), we will have
= 2 * 1 + 1 = 3 (from 0,1,2), we will have ![]() ,
, ![]() and
and ![]() , and the combined function mathematically represented as,
, and the combined function mathematically represented as, ![]() . For
. For ![]() there are a total of 3 learned parameters. Finally for each channel there will be
there are a total of 3 learned parameters. Finally for each channel there will be ![]() ,
, ![]() and
and ![]() .
.
Train Gaussian Splatting on Custom Dataset
There are multiple ways to train a Gaussian splats, you ca use,
- Gaussian Splatting official repo
- gSplats from NeRF-Studio
What is gSplat?
Gsplat is the Gaussian Splatting library that’s being used in nerf-studio directly. It is designed for efficiency. Compared to the official implementation, it reduces training memory usage by up to 4x and cuts training time by up to 15% on Mip-NeRF 360 captures, with even greater improvements possible on larger scenes.
Gsplat is optimized for large scene rendering, offering faster performance than the official CUDA backend. It includes features like batch rasterization, depth rendering, multi-GPU support, and advanced techniques like absgrad, anti-aliasing, and 3DGS-MCMC.
First we need to create a 360 degree video of the scene, after that we process the video and extract the video frames, done using video2imgs.py. Then we pass that to the COLMAP (structure from motion pipeline), to get the camera intrinsics, and extrinsics, and finally that’s being converted in the llff format. This process is done using imgs2poses.py script.
Install COLMAP
COLMAP is available as an apt package, so simple apt install works fine. if you get stuck you can install it from source, follow the official documentation, the instructions in the official docs works like a charm in Ubuntu 20.4.
$ sudo apt install colmap
After this is done you can either clone the Gsplat repository or use the below download button to download the repository with all the changes and additional files. It also has links to custom datasets.
Data Preparation
After downloading the dataset from the subscribe code button, perform the following steps,
- This command converts the video into frames and stores them inside the
output_dir. Name theoutput_diras “images”.
$ python video2imgs.py --video_path /path/to/video.mp4 --output_dir /path/to/dataset --fps <number from 1-30>
- Now, we will run COLMAP on the custom data using
imgs2poses.pyscript. You can also run COLMAP separately. Factor can be anything (generally 1to n (generally n=8) based on the original image size).
$ python imgs2poses.py --data_dir "/path/to/dataset" --factor <int>
If you want to run COLMAP separately, following are the steps,
- Click on the “New Project”, and it will show a new window with database and images. Database needs to be saved as a file, and the images are the folder where you have stored all the images.
- Next click on, Processing → Feature Extraction → Extract. It will have all the features from the images.
- Then click on Processing →Feature Matching → Run, It will perform feature matching.
- And finally click on, Reconstruction → Start Reconstruction, this will start the Structure from Motion. Based on the number of images, it can take time from minutes to hours.
- After the Reconstruction is finished, click on File → Export All Models, this will save the camera position, point clouds in .bin format. The folder will be named “0”, create a new folder named “sparse”, and place the folder “0” inside the “sparse” folder. And Voila! We are done with 50% of the work.
Start Training
Clone the gsplats repository and follow the installation instructions provided there. In our case we were able to install it properly using the .whl files provided, but you can try different methods based on your system configuration.
After the installation, go to the gsplats repository, and run the below command. --data_dir is the folder where your images and sparse folder is located. And --result_dir is the folder where the model checkpoint and ply files will be stored.
$ CUDA_VISIBLE_DEVICES=0 python examples/simple_trainer.py default --data_dir /path/to/images/folder/ --data_factor 1 --result_dir ./results/dataset
After training is over you can see the output using the below command. Although during training, it opens up “viser”, the visualization tool in a browser.
$ python examples/simple_viewer.py --ckpt /path/to/model.pt
We’ve trained the model on various scenes, both small and large, and the results are impressive, as shown below. However, there are a few important considerations to understand before starting the training process.
Smaller Scene
Larger Scene
Gaussian Splatting Limitations
Gaussian splatting is very good in terms of a real time, photo-realistic 3D reconstruction, but it comes with the cost of multiple thing,
- Too many Gaussians : You are representing a scene using millions of gaussians, and each of them has 5 parameters associated with it. So, because of this the final .ply file becomes very large (in 100-200 MB).
- Capture Every Angle : Proper data collection is crucial. This means you need to capture images from every angle—front, back, left, right, and so on. Otherwise, the scene may look great from the angle you photographed, but not as well from other perspectives.
- Saved as ply : Even though the final output can be saved using ply files, it doesn’t mean that it only contains points, it has gaussians as well. So, viewing that can only be doing using some specific websites or softwares, below are few,
- SuperSplat (Visualize + Editing)
- 3D Gaussian Splatting with Three.js (Visualize)
- Viser (Visualize)
- Splatviz (Visualize + Editing)
- Doesn’t Generate a Mesh : You can’t create a mesh from Original Gaussian Splatting implementation. To create a mesh out of a gaussian splat, you have to use “SuGaR: Surface-Aligned Gaussian Splatting for Efficient 3D Mesh Reconstruction” you can refer to this video to do so.
Key Takeaways
- No Neural Networks: Unlike NeRF or other approaches, 3DGS does not use neural networks, relying instead on mathematical optimization and tile-based rasterization.
- Data Representation: 3D scenes are represented as millions of 3D Gaussians characterized by their position, covariance, color, opacity, and spherical harmonic parameters for view-dependence.
- Optimization Pipeline: Adaptive density control refines Gaussians through pruning and densification, while the optimization process focuses on minimizing L1 loss and D-SSIM in view space.
- Tile-Based Rasterization: Efficient GPU-based rendering is achieved by culling, sorting, and processing Gaussians in parallel within screen-space tiles.
- Spherical Harmonics for View-Dependence: Gaussian colors are parameterized using Spherical Harmonics, encoding view-dependent appearance.
Conclusion
3D Gaussian Splatting (3DGS) is revolutionizing 3D graphics and vision by offering real-time, photorealistic 3D scene reconstruction without relying on neural networks. Its innovative use of 3D Gaussians and efficient rendering techniques addresses many challenges faced by traditional methods like photogrammetry and NeRF. While it has limitations, such as large file sizes and specific visualization requirements, its speed, scalability, and high-quality results make it a promising approach for applications in gaming, AR/VR, and real-time 3D content creation. Tools like gSplats further simplify its adoption, opening the door to new possibilities in 3D graphics and vision.
References
- A Comprehensive Overview of Gaussian Splatting
- Rendering in 3D Gaussian Splatting
- A thorough explanation of “3D Gaussian Splatting”, a surprisingly beautiful 3D scene reconstruction
- Machine Learning for Inverse Graphics 6.S980




100K+ Learners
Join Free OpenCV Bootcamp3 Hours of Learning